ここでベクトル
![]() を
を
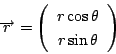
高校の数学では,
![]() が一定の円運動について速度ベクトルと加速度ベクトルが求められている.
が一定の円運動について速度ベクトルと加速度ベクトルが求められている.
ここでは![]() も角
も角![]() も時
も時![]() の関数であるとして,
速度ベクトルと加速度ベクトルを求めなければならない.
の関数であるとして,
速度ベクトルと加速度ベクトルを求めなければならない.
拓生
やってみます.
以下![]() や
や![]() は
は![]() に関する1次微分,2次微分であるとします.
に関する1次微分,2次微分であるとします.
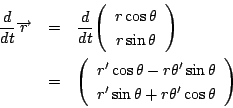
南海
この結果は
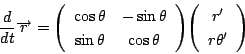
拓生

南海 ここで
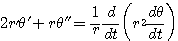
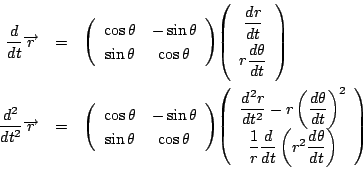
拓生
ニュートンの法則は惑星運動では
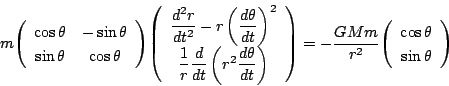
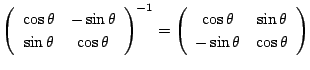 を左からかけると,
を左からかけると,
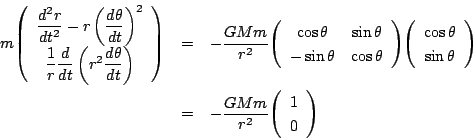
これから
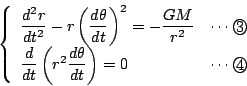
拓生
これは
南海 極方程式で表された運動の,面積速度の式を求めよう.
![]() に対し時間の変化量を
に対し時間の変化量を![]() とし.
とし.
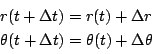
とおこう.また,動径の通過面積を![]() とする.
とする.
 時間
時間![]() から
から![]() までの間の動径の最大値と最小値を R と r とすれば
までの間の動径の最大値と最小値を R と r とすれば
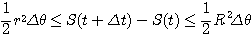
したがって
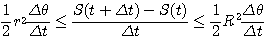
拓生 かくして面積速度一定が示されたわけです.
南海
一点注意.面積速度一定を意味する式![]() を導いた過程を見直せば,
働いている力が
を導いた過程を見直せば,
働いている力が
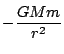 でなくても,距離
でなくても,距離![]() のみに関する任意の関数であっても,
のみに関する任意の関数であっても,
![]() が結論される.
が結論される.
つまり面積速度一定は,万有引力の法則とは独立に, 中心力のみが働くところで成立する.