次： 凸多角形と凸関数 上： オイラーの公式 前： オイラーの公式へ

いくつかの話題

南海　　 ここまで来ればド・モアブルの定理とは，指数法則

$$e^{i(\theta_1+\theta_2)}=e^{i\theta_1}e^{i\theta_2}$$

そのもであることがわかる．ド・モアブルの定理は三角関数の加法定理そのものだ．

ところで1999年の東大で次の問題が出題されている．

例 1.2.1       ［99東大前期文理］

1. 一般角 $\theta$ に対して $\sin \theta,\ \cos \theta$ の定義を述べよ．
2. (1)で述べた定義にもとづき一般角 $\alpha,\ \beta$ に対して
   $$\begin{eqnarray*} &&\sin(\alpha+\beta)=\sin \alpha\cos \beta+\cos \alpha\sin \b... ...&\cos(\alpha+\beta)=\cos \alpha\cos \beta-\sin \alpha\sin \beta \end{eqnarray*}$$
   
   
   を証明せよ．

われわれの立場から別の解ができる．

史織　　

$\cos \theta$ は $e^{i\theta}$ の実部とするのですね． すると $e^{i\theta}$ の共役は$e^{-i\theta}$ だから次の式を定義にできる．

1. 
   
   $$\cos \theta=\dfrac{e^{i\theta}+e^{-i\theta}}{2},\ \sin \theta=\dfrac{e^{i\theta}-e^{-i\theta}}{2i}$$
   
   

2. このとき
   
   $$e^{i\theta}=\cos \theta+i\sin \theta$$
   
   
   である．
   
   $$e^{i(\alpha+\beta)}=e^{i\alpha}e^{i\beta}$$
   
   
   より
   $$\begin{eqnarray*} \cos(\alpha+\beta)+i\sin(\alpha+\beta)&=& (\cos \alpha+i\sin... ...pha\sin \beta) +i(\sin \alpha\cos \beta+\cos \alpha\sin \beta) \end{eqnarray*}$$
   
   
   両辺の実部と虚部を比較して加法定理が得られる．

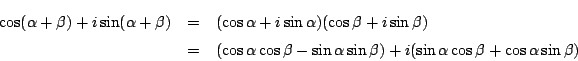
南海　　 もちろんこれは，$e^{i\theta}$の定義や指数法則の成立を示していないので 解答としては不完全だ．しかし，今話してきたことをすべて書けば一応解答にはなる．

三角関数の定義は一つではない．さらに別の観点から定義することもできる．

オイラーの公式を手にすると，二つの三角関数 $\sin \theta,\ \cos \theta$ を $e^{i\theta}$の実部と虚部として統一的につかめる．

例えば，もし

$$\dfrac{d}{d\theta}e^{i\theta}=ie^{i\theta}$$

を認めるなら

$$\begin{eqnarray*} &&\dfrac{d}{d\theta}(\cos \theta+i\sin \theta) =\dfrac{d}{d\th... ...heta\\ &=&i(\cos \theta+i\sin \theta)=-\sin \theta+i\cos \theta \end{eqnarray*}$$

より

$$\dfrac{d}{d\theta}\cos \theta=-\sin \theta,\ \dfrac{d}{d\theta}\sin \theta=\cos \theta$$

となる．

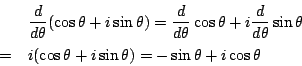
いろいろ試してみてほしい．