拓生 つまり素数は無数にあるということですね.
南海 2300年以上前になるわけだが,ユークリッドが背理法で素数が無数にあることを証明した.このユークリッドの 証明がそのまま入試問題になっている.『高校数学の方法』「論証の推進力-背理法」で紹介している. ぜひこれを見てほしい.
次に![]() は確かにいくらでも大きくなるのだが,しかしその大きさの程度は
は確かにいくらでも大きくなるのだが,しかしその大きさの程度は![]() よりも
ずっと小さく
よりも
ずっと小さく
ひとつ記号を定める.![]() は和の記号として知っている.積の記号を
は和の記号として知っている.積の記号を![]() とする.例えば
とする.例えば
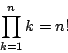
この証明のために,『初等整数論』で既出の関係式であるが次の等式を補題としてあらかじめ 示しておこう.
![]() を相異なる素数とする.
実数
を相異なる素数とする.
実数 ![]() を越えない自然数のなかで
を越えない自然数のなかで
![]() のいずれでも
割り切れないものの個数は次式で与えられる.
のいずれでも
割り切れないものの個数は次式で与えられる.
![\begin{eqnarray*}
&&[x]
-\left[\dfrac{x}{p_1}\right]-\left[\dfrac{x}{p_2}\righ...
...1)^r\left[\dfrac{x}{p_1p_2\cdots p_r}\right]\quad \cdots\maru{1}
\end{eqnarray*}](images/img751.png)
拓生 『初等整数論』を参考に数学的帰納法で示します.
証明
![]() に関する数学的帰納法で証明する.
に関する数学的帰納法で証明する.
![]() のときは
のときは
![]() のなかで
のなかで ![]() の倍数は
の倍数は
![]() のとき
のとき![]() が成立するとする.
が成立するとする.
![]() とし,さらに
とし,さらに ![]() が追加されたとする.
このときは,さらに
が追加されたとする.
このときは,さらに ![]() の倍数
の倍数
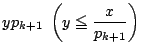 を除かなければならない.そのうち
を除かなければならない.そのうち ![]() が
が
![]() で割り切れるものは
すでに除かれているので,新たに除くべきものの個数は,
で割り切れるものは
すでに除かれているので,新たに除くべきものの個数は,
![]() を越えない整数のなかで
を越えない整数のなかで
![]() で割り切れないものの個数である.ゆえに求める個数は
で割り切れないものの個数である.ゆえに求める個数は
![\begin{eqnarray*}
&&[x]-\left[\dfrac{x}{p_1} \right]-\left[\dfrac{x}{p_2} \righ...
...cdots
+(-1)^{k+1}\left[ \dfrac{x}{p_1p_2\cdots p_{k+1}}\right]
\end{eqnarray*}](images/img764.png)
ゆえに ![]() のときも成立し,題意が示された.□
のときも成立し,題意が示された.□
南海 微積から補題をもう一つ.
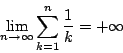
拓生 これはできます.
証明
関数![]() は単調減少なので
は単調減少なので
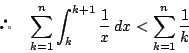
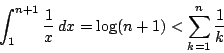
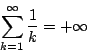
南海 以上の準備をして定理7を証明しよう.
定理7の証明
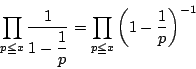
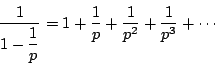
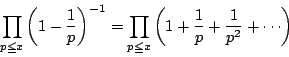
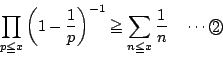
ここで補題4より,![]() のとき
のとき![]() の右辺は発散する.
の右辺は発散する.
もし
![]() が有限であれば,
が有限であれば,![]() のとき
のとき![]() の左辺は
有限個の素数にわたる和となり収束する.
これは矛盾なので
の左辺は
有限個の素数にわたる和となり収束する.
これは矛盾なので
![]() が示された.
が示された.
![\begin{eqnarray*}
\pi(x)&\le&r+[x]
-\left[\dfrac{x}{p_1}\right]-\left[\dfrac{x...
...right]-\cdots
+(-1)^r\left[\dfrac{x}{p_1p_2\cdots p_r}\right]
\end{eqnarray*}](images/img781.png)
補題3の和の項数は![]() である.
である.
![]() なので,あわせて
なので,あわせて
![]() がなりたつ.
したがって
がなりたつ.
したがって
![\begin{eqnarray*}
&&[x]-\left[\dfrac{x}{p_1}\right]-\left[\dfrac{x}{p_2}\right]...
...ots p_r}\\
&=&2^r+x\prod_{k=1}^r\left(1-\dfrac{1}{p_k}\right)
\end{eqnarray*}](images/img785.png)
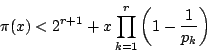
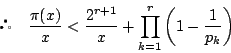
ここで![]() を
を
![]() である最大のものにとる.このとき
である最大のものにとる.このとき
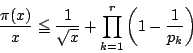
![]() のとき
のとき![]() である.したがって(1)で示したように
である.したがって(1)で示したように
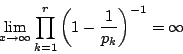
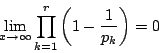
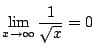 とあわせて
とあわせて