このような場合,まず実験して,![]() の一定の範囲にある素数の個数を求めていくことが大切だ.
自分でプログラムを組んで,書き出していくのがいちばんよい.エラトステネスの篩の方法は
プログラムを書く練習のいちばん初歩の問題だ.
の一定の範囲にある素数の個数を求めていくことが大切だ.
自分でプログラムを組んで,書き出していくのがいちばんよい.エラトステネスの篩の方法は
プログラムを書く練習のいちばん初歩の問題だ.
ただ大きなところまで計算すると結構時間がかかる.そこで今回は次のところに載っている表を参考にしよう. アメリカのテネシー大学の先生が展開している「The Prime Pages」だ. URLは http://primes.utm.edu/ なので見てほしい.
この中に次のような表が載っている. http://www.utm.edu/research/primes/howmany.shtml このページを見るときは,ブラウザソフトの表示文字種「エンコード」を「Unicode(UTF-7)」にするときれいになる.
ここでは多くの結果が証明なしに紹介されている.
拓生 100までだと規則性があるようには見えないけれど,1000になるとなんとなく直線? いや少し上に凸なようにも見えます.
http://www.utm.edu/research/primes/gifs/pi1000000.gif
1000000では,やや上に凸なきれいな曲線です.
南海
多くの人が![]() の性質を研究した.
の性質を研究した.
拓生
![]() で
で
![]() のときの表に次の値を書き加えてみます.
のときの表に次の値を書き加えてみます.

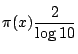 になるということです.
になるということです.
南海
そう.このようなことを昔の人はいろいろ調べたのだ.計算機のない時代に手計算で調べたのだ.
![]() は約
は約![]() なのでこの計算では
なのでこの計算では
![]() はほぼ
はほぼ 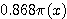 ということになる.
もっと
ということになる.
もっと![]() を大きくとるとどのような値に収束するか,これをいろいろと推測したのだ.
を大きくとるとどのような値に収束するか,これをいろいろと推測したのだ.
その結果1801年にルジャンドルは
さらにこれとは独立にガウスは
拓生 予想はいろいろあったのでしょうが,実質的な進展はどうだったのでしょうか.
南海 あのチェビシェフが1850年に次のことを示した.これも先のページにある.次のようにかかれている.
Tchebycheff made the first real progress toward a proof of the prime number theorem in 1850, showing there exist positive constantssuch that
and that ifhad a limit, then its value must be one.
今日はこのチェビシェフの定理の前半を示そう.
正の定数![]() で,
で,![]() に対して
に対して
これを示すためにひとつ補題を証明しておこう.
自然数 ![]() の素因数分解に含まれる素数
の素因数分解に含まれる素数 ![]() の個数は,
の個数は,
![\begin{displaymath}
\sum_{l=1}^{[\log_pn]}\left[\dfrac{n}{p^l}\right]
\end{displaymath}](images/img816.gif)
証明
![]() は
は![]() となる最大の
となる最大の![]() の値である.
の値である.
1から![]() までの自然数のなかでちょうど
までの自然数のなかでちょうど![]() で割り切れるものの個数は
で割り切れるものの個数は
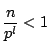 となり
となり
![$\left[\dfrac{n}{p^l} \right]=0$](images/img823.png) である.したがって求める個数は
である.したがって求める個数は
![\begin{eqnarray*}
&&\sum_{l=1}^{[\log_pn]}
l\left(\left[\dfrac{n}{p^l} \right]-\...
... \right]\\
&=&\sum_{l=1}^{[\log_pn]}\left[\dfrac{n}{p^l}\right]
\end{eqnarray*}](images/img824.gif)
定理8の証明
![]() を正整数として,整数
を正整数として,整数
![]() である素数に対して
である素数に対して
![]() の素因数分解に含まれる素数
の素因数分解に含まれる素数 ![]() の個数は,
補題5より
の個数は,
補題5より
![\begin{displaymath}
\sum_{l=1}^{[\log_p(2m)]}\left(\left[\dfrac{2m}{p^l} \right]-2\left[\dfrac{m}{p^l}\right]\right)
\end{displaymath}](images/img829.png)
![\begin{displaymath}
\left[\dfrac{2m}{p^l} \right]-2\left[\dfrac{m}{p^l}\right]=
...
...1&\biggl( \dfrac{p^l}{2}\le r <p^l \biggr)
\end{array}\right.
\end{displaymath}](images/img830.png)
![\begin{displaymath}
\sum_{l=1}^{[\log_p(2m)]}\left(\left[\dfrac{2m}{p^l} \right]-2\left[\dfrac{m}{p^l}\right]\right)
\le [\log_p(2m)]
\end{displaymath}](images/img831.png)
これから
![\begin{displaymath}
\dfrac{(2m)!}{m!m!}\le \prod_{p \le 2m}p^{[\log_p(2m)]}
\end{displaymath}](images/img832.gif)
一方
![]() であるから
であるから
![\begin{displaymath}
\prod_{p \le 2m}p^{[\log_p(2m)]}\le (2m)^{\pi(2m)}
\end{displaymath}](images/img834.gif)
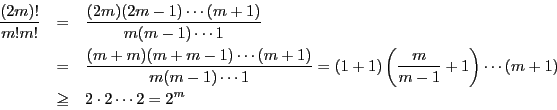
次に![]() に対して
に対して
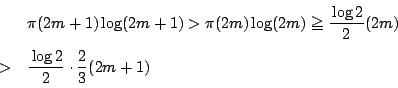
したがって整数![]() に対して
に対して
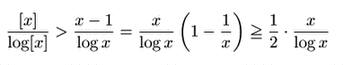
したがって
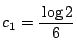 とおけばよい.
とおけばよい.
次に,
![]() の範囲の素数は
の範囲の素数は
![]() の分母を割らない.よって
の分母を割らない.よって
![]() は
は
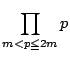 で割り切れる.つまり
で割り切れる.つまり
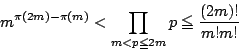
これから
ところが
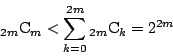
![]() に対して
に対して
![\begin{eqnarray*}
\pi(2y)-\pi(y)&=&\pi([2y])-\pi([y])\\
&\le&\pi(2[y]+2)-\pi([y...
...
&<&2\log 2\dfrac{[y]}{\log [y]}+2<(2\log 2+2)\dfrac{y}{\log y}
\end{eqnarray*}](images/img860.png)