次数だけの根があることは
(1+2i)x2+(2+i)x-3(1+i)=0
南海 そうだ.ただし,6次方程式に6個の根があることが重要なのではない. 基本的なことは,複素数を係数にもつ方程式の根は複素数のなかに存在する,ということだ.
史織
一つの根![]() があれば,因数定理によって方程式が
があれば,因数定理によって方程式が
![]() と因数分解できる.
と因数分解できる.
![]() も
も![]() の多項式なので,
の多項式なので,![]() をまた因数分解して,次々に分解していけばよいのですね.
をまた因数分解して,次々に分解していけばよいのですね.
6次方程式に6個あることは,少なくとも一つの根が存在することの結果なのですね.
南海
![]() を複素数係数の
を複素数係数の![]() 次多項式とする.
次多項式とする.
![]() のように
のように![]() と置いて得られる方程式を代数方程式と呼ぼう.
と置いて得られる方程式を代数方程式と呼ぼう.
![]() 次の代数方程式には必ず根があること,その結果として
次の代数方程式には必ず根があること,その結果として![]() 個の根があることを,
実際に方程式を解くことなく保証する.これがいわゆる代数学の基本定理だ.
個の根があることを,
実際に方程式を解くことなく保証する.これがいわゆる代数学の基本定理だ.
史織 しかしどのような根拠によって,このようなことが示されるのでしょうか.
南海 証明方法は実はいくつかある. いちばん一般的な方法は,実数の連続性といわれる性質と複素数の極形式 に 存在の根拠を求めるものだ.
それだけではもちろん何のことかわからないだろうから, 代数学の基本定理と実数,複素数の基本について最初から少しずつ考えてみよう.
代数方程式に一つの根![]() が存在すれば因数定理によって
が存在すれば因数定理によって
史織 この定理の証明は厳密には数学的帰納法ですね.
![]() のとき.
のとき.![]() とすると,方程式は
とすると,方程式は![]() .
.
![]() より
より![]() なので,
なので,
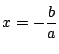 という根がただ一つ存在する.
という根がただ一つ存在する.
![]() 次で成立するとする.
次で成立するとする.![]() の両辺の次数と最高次の係数を比較して
の両辺の次数と最高次の係数を比較して
![]() が
が![]() 次式で,
次式で,![]() の項の係数は
の項の係数は![]() であることがわかる.
数学的帰納法の仮定から
であることがわかる.
数学的帰納法の仮定から![]() は重複度を含めてちょうど
は重複度を含めてちょうど![]() 個の複素数根
をもつ.これを
個の複素数根
をもつ.これを
![]() とすると,
とすると,
南海 さて,「複素数は本当に存在するのか」で次のように書いた.
「代数学の基本定理」は代数方程式を解くことに関しては複素数より大きい世界は要らない, ということを意味している.これまではそうではなかった.は,係数は整数だが,その根は整数でなく有理数だし,
なら根は無理数だ.実数の世界まで広げなければ根がない. このように,これまでは係数が属する世界より外の広い世界を考えなければ 根がないということが起こったが, 複素数係数の代数方程式のすべて根は複素数の中に存在するので, 代数方程式を解くということでは,これより広い数の世界は要らないのだ. このことを「複素数は代数的に閉じている」という.その意味で複素数は十分に広い世界なのだ.】
これはここではもう少し正確に述べなければならない.
自然数から整数,整数から有理数,実数から複素数への世界の広がりは, 根が存在するように代数的に広げていくことで実現される.しかし,実数は 有理数に有理数係数の代数方程式の実数の根を付け加えた数の集合より大きいのだ.
有理数係数の代数方程式の根になる数を代数的数と呼ぶ.
代数的数は複素数の範囲で考える.![]() も代数的数だ,代数的でない実数を超越数という.
実数は代数的な実数の集合より大きい集合なのだ.円周率
も代数的数だ,代数的でない実数を超越数という.
実数は代数的な実数の集合より大きい集合なのだ.円周率![]() や自然対数の底
や自然対数の底![]() は
超越数であって代数的数ではない.
は
超越数であって代数的数ではない.
史織 証明は難しいのですか.
南海 現在でも,超越性が示されている実数はほんの僅かであり, 与えられた数が超越数であるかどうかを調べるのはたいへん難しい.
史織
![]() が無理数であることの証明は,2003年の大阪大学後期の試験問題にありました.
が無理数であることの証明は,2003年の大阪大学後期の試験問題にありました.
南海
そう.![]() や
や![]() が無理数であることの証明は高校範囲でできる.
が無理数であることの証明は高校範囲でできる.
![]() が無理数であることの証明を例題にしておこう.(1)〜(3)は入試問題.(4)(5)はその応用だ.
が無理数であることの証明を例題にしておこう.(1)〜(3)は入試問題.(4)(5)はその応用だ.
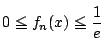 が成り立つことを示せ.
が成り立つことを示せ.
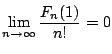 を示せ.
を示せ.
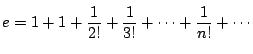 を示せ.
を示せ.
史織
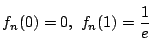 であるから
であるから
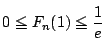 .つまり
.つまり
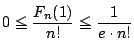 .
.
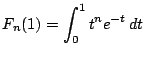 なので
なので
![\begin{eqnarray*}
F_n(1)&=&\left[-t^ne^{-t} \right]_0^1+n\int_0^1t^{n-1}e^{-t}\,dt\\
&=&-\dfrac{1}{e}+nF_{n-1}(1)
\end{eqnarray*}](images/img53.png)
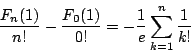
ここで
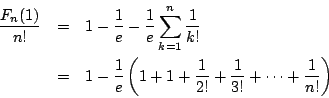
(2)から
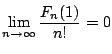 なので
なので
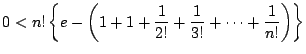 は明らかである.
次に
は明らかである.
次に
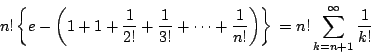
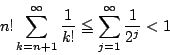
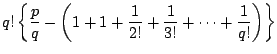 は整数なので,これは矛盾である.よって
は整数なので,これは矛盾である.よって
1744年,オイラーはこの練習問題のようにして![]() の無理数性を示した.
さらに,1873年,エルミートは
の無理数性を示した.
さらに,1873年,エルミートは![]() が超越数であることを証明した.
これに対して,
が超越数であることを証明した.
これに対して,![]() が無理数であることを示したのはランベルト(1761年)であり,
最終的にリンデマンが
が無理数であることを示したのはランベルト(1761年)であり,
最終的にリンデマンが![]() が超越数であること証明した(1882年).
リンデマンはエルミートの方法を発展させ,
が超越数であること証明した(1882年).
リンデマンはエルミートの方法を発展させ,![]() の超越性を示した.
の超越性を示した.