![]() 平面上の有界閉領域
平面上の有界閉領域![]() とは,
十分大きい円盤をかけばその中に
とは,
十分大きい円盤をかけばその中に![]() が入り.
が入り.![]() の無限部分集合の集積点がすべて
の無限部分集合の集積点がすべて![]() に
属することをいう.このとき
に
属することをいう.このとき
証明
![]() を固定すれば
を固定すれば![]() の関数になり
の関数になり![]() を固定したとき
を固定したとき![]() が
が![]() の閉集合にあることは明らかである.
したがって
の閉集合にあることは明らかである.
したがって![]() を固定するたびに最大値
を固定するたびに最大値![]() が存在する.これは
が存在する.これは![]() の連続関数である.また,
の連続関数である.また,
![]() とおけば
とおけば![]() は実数の集合の中の閉集合である.したがって
は実数の集合の中の閉集合である.したがって![]() の関数としての
の関数としての![]() に最大値
に最大値![]() がある.
がある.![]() が連続だから,先に y を固定して得られる最大値
が連続だから,先に y を固定して得られる最大値![]() と等しく,
これが.
と等しく,
これが.![]() の
の![]() における最大値である.
における最大値である.
最小値についても同様である.□
以下複素数係数の多項式を,変数を![]() で,係数を
で,係数を![]() で表すことにする.
で表すことにする.
代数学の基本定理を三段階に分けて証明する.最初の二段階を補題として示す.
証明
![]() は複素数平面全体で定義された
は複素数平面全体で定義された![]() と
と![]() の連続関数である.
の連続関数である.
そこで
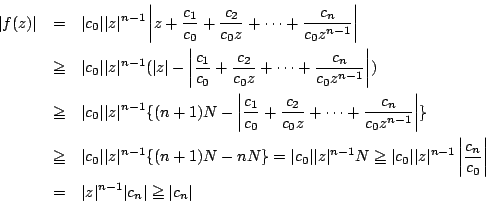
これは![]() の絶対値を十分大きくとれば,関数値の絶対値は定数項の絶対値
の絶対値を十分大きくとれば,関数値の絶対値は定数項の絶対値![]() より大きくできる
ということで,それ自体当然のことである.
より大きくできる
ということで,それ自体当然のことである.
補題 2
![]() は前補題の
は前補題の![]() とする.
関数
とする.
関数
![]() の有界閉領域
の有界閉領域
![]() における最小値は,関数
における最小値は,関数![]() の
の
![]() 全体における最小値である.
全体における最小値である.
証明
![]() が関数
が関数![]() の
の![]() における最小値とする.任意の
における最小値とする.任意の![]() について
について![]() なら
なら![]() .
.
![]() なら前補題から
なら前補題から
![]() である.□
である.□
基本定理1の証明
関数![]() の
の![]() における最小値は定理2により存在する.その最小値を
における最小値は定理2により存在する.その最小値を![]() とする.このとき
とする.このとき
![]() として矛盾を示す.最小値を与える
として矛盾を示す.最小値を与える![]() を
を![]() とする.つまり
とする.つまり
なぜそれが可能か.
![]() の最大値を
の最大値を![]() とし,
とし,![]() とおくと
とおくと
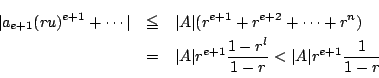
 となるようにとればよい.両辺
となるようにとればよい.両辺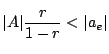 なので,
このような
なので,
このような
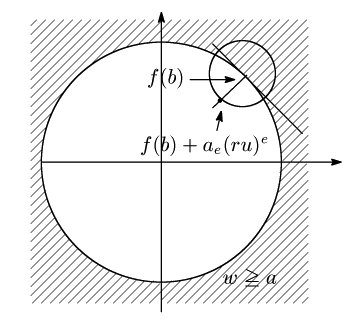
ここで![]() によって複素数平面から複素数平面への関数を考える.
によって複素数平面から複素数平面への関数を考える.
角![]() が0から
が0から![]() まで変化すると
まで変化すると
![]() は
は![]() の周りを
の周りを![]() 回まわる.
回まわる.
![]() はつねに
はつねに![]() をみたす領域内になければならない.ところが
をみたす領域内になければならない.ところが
![]() が図のように
が図のように![]() をとおり円
をとおり円![]() と垂直な直線上に来たとき,
と垂直な直線上に来たとき,![]() から
から![]() は
は
![]() 内にはあり得ない.
内にはあり得ない.
これは![]() が
が![]() の最小値であることと矛盾する.
の最小値であることと矛盾する.
したがって![]() となり確かに
となり確かに![]() となる
となる![]() が存在する.□
が存在する.□