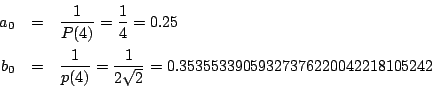そこで今日は,円周率を実際に式に表し値を求めるさまざまな方法を, 高校数学として可能な範囲で考えよう.
拓生
まず円周率![]() の定義です.
の定義です.
その値は
南海 そう.
日常の目的には![]() や
や![]() を用いれば十分で,もう少し精度の高い数値が必要な技術系では
を用いれば十分で,もう少し精度の高い数値が必要な技術系では
![]() や
や ![]() などを使用することが多い.
天気予報や人工衛星などの計算では30桁程度の値を使用している.
などを使用することが多い.
天気予報や人工衛星などの計算では30桁程度の値を使用している.![]() も覚えやすく精度が高い分数である.
も覚えやすく精度が高い分数である.
ドイツの数学者ルドルフ・ファン・コイレンは1600年代に35桁目まで ![]() の正しい値を計算した.
彼の墓標にはこの値が刻まれている.ドイツでは彼の名にちなんで円周率をルドルフ数と呼ぶそうだ.
スロベニアの数学者ユリー・ベガは1789年に140桁まで正しい値を求め,37桁目までが正しかった.
この記録はその後50年破られることがなかった.
の正しい値を計算した.
彼の墓標にはこの値が刻まれている.ドイツでは彼の名にちなんで円周率をルドルフ数と呼ぶそうだ.
スロベニアの数学者ユリー・ベガは1789年に140桁まで正しい値を求め,37桁目までが正しかった.
この記録はその後50年破られることがなかった.
円周率は人間が世界から見いだした定数で,やはり人間の歴史とともにある.
円周率を算出することは、アルキメデスが円に接する正多角形の周長を 求めることにより始まった. まずアルキメデスの方法を整理しよう.
円周率の定義から,半径![]() の円の円周がちょうど
の円の円周がちょうど![]() になる.
そこで半径
になる.
そこで半径![]() の円に内接する正
の円に内接する正![]() 角形の周の長さを
角形の周の長さを![]() ,
外接する正
,
外接する正![]() 角形の周の長さを
角形の周の長さを![]() とおこう.
とおこう.
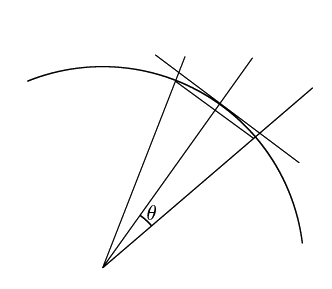 拓生
まずこれを求めてみます.
正
拓生
まずこれを求めてみます.
正![]() 角形の隣りあう2つの頂点と円の中心がなす角の
角形の隣りあう2つの頂点と円の中心がなす角の![]() を
を![]() とおく.
とおく.
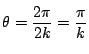 になる.
になる.
したがって
内接正![]() 角形の1辺は
角形の1辺は
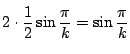 .
外接正
.
外接正![]() 角形の1辺は
角形の1辺は
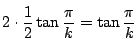 になる.
になる.
南海
だから,ここでさらに正多角形の各辺を2分割して正![]() 角形にするとそれぞれ周の長さは
角形にするとそれぞれ周の長さは
ここでもし![]() を
を![]() で表すことができれば,最初は正三角形や正四角形から
はじめて,次々に正六角形や正八角形,正十二角形や正十六角形,
で表すことができれば,最初は正三角形や正四角形から
はじめて,次々に正六角形や正八角形,正十二角形や正十六角形,![]() としたときの内接正多角形と
外接正多角形の周の長さを,その関係式から求めていくことができる.
としたときの内接正多角形と
外接正多角形の周の長さを,その関係式から求めていくことができる.
拓生
とりあえず![]() の和と積を作ってみます.簡単のために
の和と積を作ってみます.簡単のために
![]() とおきます.
とおきます.
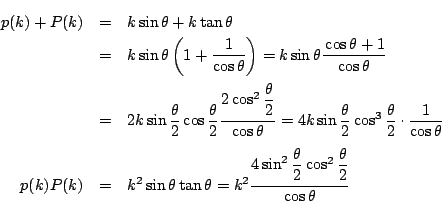
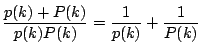 だから
だから
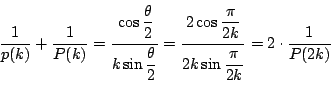
![]() がわかりません.
がわかりません.
南海 ここは次のようにすればよい.
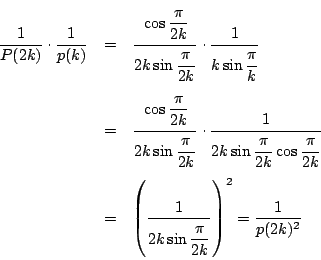
拓生
つまり
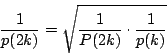
南海
とすると,最初に任意の正![]() 角形を作り,そこから順に倍々に増やしていって,
角形を作り,そこから順に倍々に増やしていって,![]() となったときを
考える.
となったときを
考える.
これで計算して![]() を求めていけば,その逆数が内接,外接正多角形の周長だ.
これは,円周に収束する.これで任意の精度で円周率が求まる.
を求めていけば,その逆数が内接,外接正多角形の周長だ.
これは,円周に収束する.これで任意の精度で円周率が求まる.
アルキメデスは正六角形から始めたらしい.
拓生
半径![]() の円に内接する正六角形の周は
の円に内接する正六角形の周は
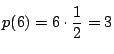 .また外接正六角形は
一辺が
.また外接正六角形は
一辺が
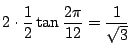 なので
なので
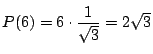 .
.
これから![]() と
と![]() を求め,漸化式によって
を求め,漸化式によって![]() と
と![]() から順に求めていく.その逆数が
外からと内からの円周の近似,つまりは円周率の近似です.
から順に求めていく.その逆数が
外からと内からの円周の近似,つまりは円周率の近似です.
この場合
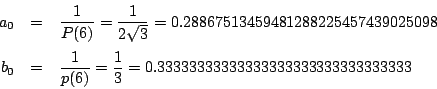
電卓を用いていくつか計算してみました.

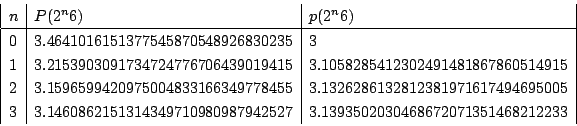
南海
![]() ということは正12角形の場合だ.
ということは正12角形の場合だ.
次に![]() で正方形から始めてみよう.
で正方形から始めてみよう.
拓生 この場合