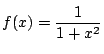 です.
です.
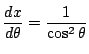 ですから
ですから
いつもこのようになります.
南海
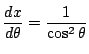 をよく見てみると
をよく見てみると
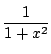 であることを意味している.
であることを意味している.
拓生
つまり![]() の逆関数の導関数ですか.
の逆関数の導関数ですか.
南海
そうだ.
いずれにせよ
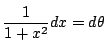 であるから,不定積分
であるから,不定積分
ところが一方,![]() に対して
に対して
![\begin{eqnarray*}
\dfrac{\pi}{4}&=&\int_0^1\dfrac{1}{1+x^2}\,dx\\
&=&\int_0^1(1...
...right]_0^1\\
&=&1-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+\cdots
\end{eqnarray*}](images/img971.png)
これがいわゆる「ライプニッツの公式」だ.ただし発見者はライプニッツではないらしい.
もちろん,![]() でなければ等比級数は収束しないのに0から1まで積分してよいのかとか,
無限級数で表される関数の定積分と,各項の定積分の和とは一致するのかとか,の問題がある.
これはいずれも肯定的に解決されるがそれについては大学で学んでほしい.
例えば『解析概論』のような解析の基本書に載っている.
でなければ等比級数は収束しないのに0から1まで積分してよいのかとか,
無限級数で表される関数の定積分と,各項の定積分の和とは一致するのかとか,の問題がある.
これはいずれも肯定的に解決されるがそれについては大学で学んでほしい.
例えば『解析概論』のような解析の基本書に載っている.
※ 後に表した『解析基礎』のなかの「積分の方法」−「広義積分」にもある.
このライプニッツの公式は,級数としての収束はあまりよくない.
東大の問題では無限級数の問題を回避するとともに,下からの評価を出すため次のような解答を作った.
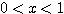 では
では 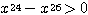 のように,
のように, 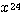 の項以下の和はは正なので,
の項以下の和はは正なので,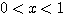 において
において
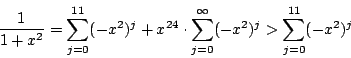
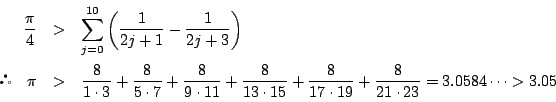
拓生 円周率を早く求めるのにいい方法はないのでしょうか.
南海 もちろんいっぱいある.ウエブ上を検索すればいくつもの公式が見つかる. その一つを紹介しよう.
先に「スロベニアの数学者ユリー・ベガは1789年に140桁まで正しい値を求め,
37桁目までが正しかった」と書いたが,彼の用いたのは次の公式で,これは
ジョン・マチンが1706年に発表したものだ.
拓生 どうしてこんな式を見つけたのでしょう.
南海
![]() の加法定理からだが,今風には次の複素数の展開からわかる.
の加法定理からだが,今風には次の複素数の展開からわかる.
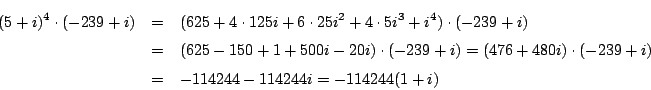
ここで
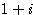 の偏角は
の偏角は 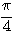 なので,これは
なので,これは
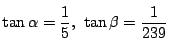 なので
なので
拓生 この節の始めの式を不定積分に書けば
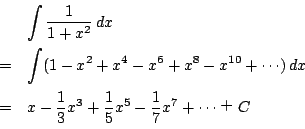
代入するものが小さいので早く収束して有効数字が大きいものが得られる.
南海 そうなんだ. この式は1949年にENIACで2037桁を計算する際に使用され,今でも収束が速いものとして知られている.
少しやってみよう.
 に
に
![]() を代入して4倍すると,
を代入して4倍すると,
拓生
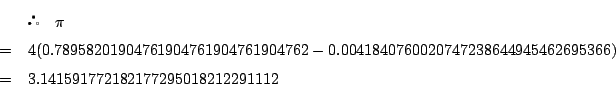
確かに一気に![]() まで来ました.
まで来ました.