拓生
ド・モアブルの定理とは,すべての整数![]() に対し
に対し
南海
ド・モアブルの定理の本質的な部分はオイラーの公式
ド・モアブルの定理の右辺は![]() の形なので
二項定理で展開することができる.
の形なので
二項定理で展開することができる.
実数部と虚数部をまとめると,
拓生
![]() をチェビシフの多項式と呼び,
をチェビシフの多項式と呼び,![]() の
の![]() 次式で
次式で![]() の係数は
の係数は![]() になる.
になる.
南海
![]() もチェビシフの多項式ということもあるし,もう少し違う形でいうこともある.
これについては『チェビシェフの多項式』を見てほしい.
これは本当に有用なもので,そこから導かれる結果は高校数学ではもっとも深いものだろう.
もチェビシフの多項式ということもあるし,もう少し違う形でいうこともある.
これについては『チェビシェフの多項式』を見てほしい.
これは本当に有用なもので,そこから導かれる結果は高校数学ではもっとも深いものだろう.
さて,今回はこのド・モアブルの定理とチェビシェフの多項式のうち,虚数部分から得られる 三角関数の多項式を用いる.
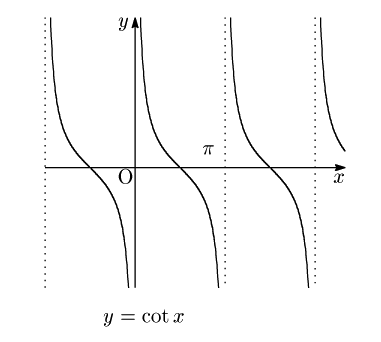
もう一つ,ここでは![]() の逆数が用いられる.
の逆数が用いられる.
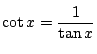 とおいて,これを
「コタンジェント」と呼ぶ.そのグラフは次のようになる.
とおいて,これを
「コタンジェント」と呼ぶ.そのグラフは次のようになる.
拓生
南海 ド・モアブルの定理の右辺を二項定理で展開し,両辺の虚数部分をとる.
拓生
二項定理により右辺は
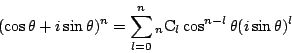
南海
![]() が偶数か奇数かで最後の項は変わってくるが,
奇数の項をまとめて左辺の虚数部分と等値すると.
が偶数か奇数かで最後の項は変わってくるが,
奇数の項をまとめて左辺の虚数部分と等値すると.
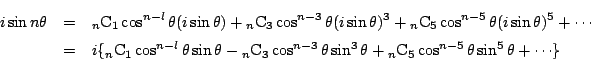
南海
![]() で
で![]() とする.
とする.![]() に各
に各
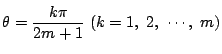 を代入する.
を代入する.
このとき左辺![]() は0で,
は0で,![]() は0でない.よってこれらの
は0でない.よってこれらの![]() に関して
に関して
いま
![]() とおくと
とおくと![]() は
は
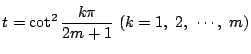 はこの
はこの
拓生
![]() 個の
個の
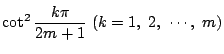 が満たす
が満たす![]() 次の方程式ですか.
根と係数の関係が使えますね.
次の方程式ですか.
根と係数の関係が使えますね.
南海
![]() の係数について何が言えるか.
の係数について何が言えるか.
拓生
![]() 次の方程式の最高次数の係数は
次の方程式の最高次数の係数は
![]() ,
,
![]() 次の項の係数は
次の項の係数は
![]() です.
です.
だから,
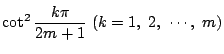 をすべて加えるとこれが
をすべて加えるとこれが![]() 個の根の和なので
根と係数の関係によって
個の根の和なので
根と係数の関係によって
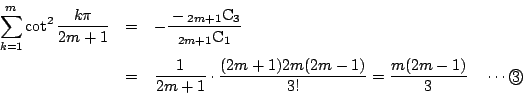
確かにこれは![]() の関係式ですが,ここから何が言えるのでしょうか.
の関係式ですが,ここから何が言えるのでしょうか.
南海
これから,ある級数の収束とその和を求める.三角関数の基本的な不等式
拓生
今は![]() を考えているので
を考えているので
![]() は
は
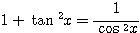 と同様に
と同様に
南海
なかなか察しがよい.![]() の左辺の各項にこの不等式を適用すると
の左辺の各項にこの不等式を適用すると
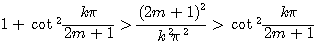
これを![]() について
について![]() から
から![]() まで加える.
まで加える.
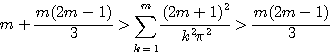
両辺に
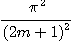 をかけると
をかけると
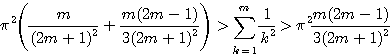
ここで![]() をとる.
をとる.
拓生
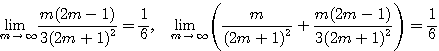
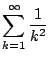 は収束し
は収束し
南海
円周率![]() を明示的に無限級数で表す公式でオイラー(1707〜82)が発見した.
を明示的に無限級数で表す公式でオイラー(1707〜82)が発見した.
もっともオイラーはもっと違う方法でこの公式に到達したらしい.『ド・モアブルの定理からオイラーの公式へ』
で紹介したが,![]() は
は
一方![]() となる
となる![]() は
は
![]() なので
なので
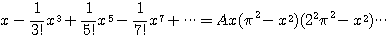
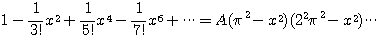
定数項を比較して
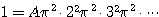
右辺の定数項は
![]() .右辺の
.右辺の![]() の係数は,これらの積から
一つずつ落としたものなので
の係数は,これらの積から
一つずつ落としたものなので
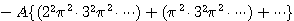
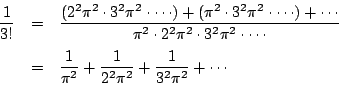
これから
このように考えたらしい.すばらしい直感だ.