 懸垂線
懸垂線
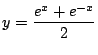 を
を
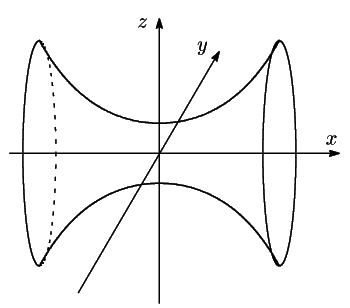
南海 ついでに懸垂線が現れる曲面を紹介しよう
 懸垂線
懸垂線
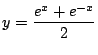 を
を![]() 軸の周りに回転した回転面を懸垂面という.
軸の周りに回転した回転面を懸垂面という.
耕一 どこかで見たことがあります.
 南海
2つの円形の針金の輪を作りシャボン玉の液で膜を作ったときの面だ.
南海
2つの円形の針金の輪を作りシャボン玉の液で膜を作ったときの面だ.
![]() での断面
での断面
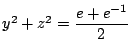 を固定する.
を固定する.
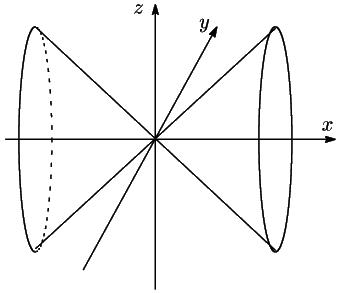
この2つの円の間に張られる面はいろいろできる.次のような円錐もある.
両端を![]() での断面
での断面
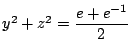 に固定したさまざまの曲面の中で
側面の面積が最小になるものが懸垂面なのだ.これが懸垂面を特徴づける.
に固定したさまざまの曲面の中で
側面の面積が最小になるものが懸垂面なのだ.これが懸垂面を特徴づける.
耕一 証明は難しいのですか.
南海 やや高校範囲を越えるのでここではできない.高校範囲で示せるようになったら証明も紹介したい.