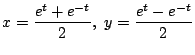 という媒介変数表示をもつ.
という媒介変数表示をもつ.
双曲線
![]() は,実数
は,実数![]() を用いて
を用いて
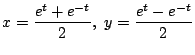 という媒介変数表示をもつ.
という媒介変数表示をもつ.
耕一
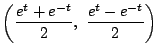 は
は
さらに相加相乗平均の不等式から
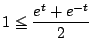 ,かつ
,かつ
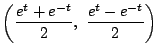 は
は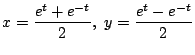 と表されます.
と表されます.
ということでいいでしょうか.
南海
同じ二次曲線である円
![]() の媒介変数表示として
の媒介変数表示として
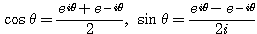
耕一
双曲線
![]() は,実数
は,実数![]() を用いて
を用いて
ということは,この2つは![]() と似ているということですか.
と似ているということですか.
南海
その通り.実は
![]() のことを三角関数というのにならって,
のことを三角関数というのにならって,
耕一
双曲線の媒介変数表示になっていたということは
 南海
そうだ.さらに,三角関数との対比で双曲線関数の性質を調べよう.
南海
そうだ.さらに,三角関数との対比で双曲線関数の性質を調べよう.
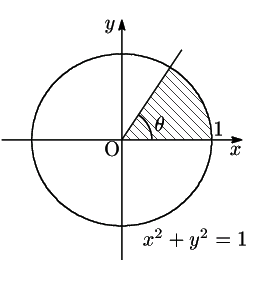
三角関数の角![]() に対して
に対して
![]() は単位円の斜線部分の面積だった.
は単位円の斜線部分の面積だった.
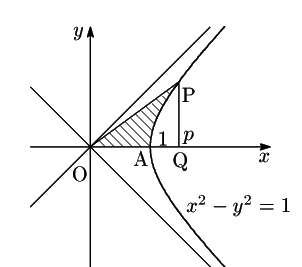 それに対して第1象限にある双曲線
それに対して第1象限にある双曲線![]() 上の点
上の点
![]() をとる.また
をとる.また
![]() とする.
また点
とする.
また点![]() から
から![]() 軸に降ろした垂線の足を
軸に降ろした垂線の足を
![]() とする.
点
とする.
点![]() に対応する媒介変数値を
に対応する媒介変数値を![]() とする.線分
とする.線分
![]() と,
点
と,
点![]() と点
と点![]() で切り取られる
で切り取られる![]() の弧とで囲まれた図形の面積
の弧とで囲まれた図形の面積![]() がちょうど
がちょうど![]() となる.
となる.
耕一
やってみます.
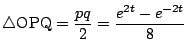 であり,さらに
であり,さらに
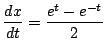 です.
です.
南海
![]() は
は![]() に対応して固定されているが,この
に対応して固定されているが,この![]() と媒介変数
と媒介変数![]() をあえて混同している.
わかっていてそうするのは構わない.
をあえて混同している.
わかっていてそうするのは構わない.
耕一 本当は文字を変えるのですが,結局同じことになります.
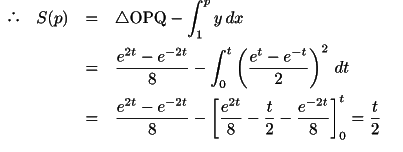
確かになりました.
ここで質問です.もともとラジアンの定義は円弧でした.双曲線の場合弧![]() の長さは
の長さは![]() でしょうか.
でしょうか.
円の場合は0から![]() までの弧長は
までの弧長は
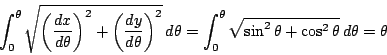
南海
どうなるかやってみよう.弧![]() の長さを
の長さを![]() としよう.
としよう.
耕一
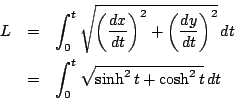
南海 では加法定理はどうだろう.
耕一
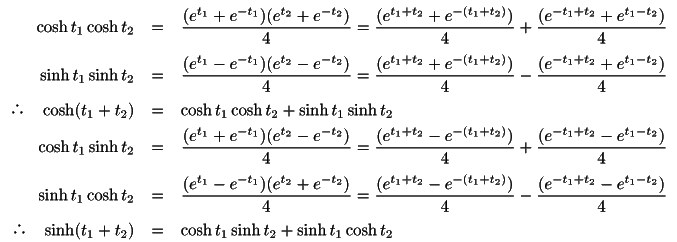
ついでにすでに計算はしていますが