上: 縮閉線
前: 双曲線の場合
上: 縮閉線
前: 双曲線の場合
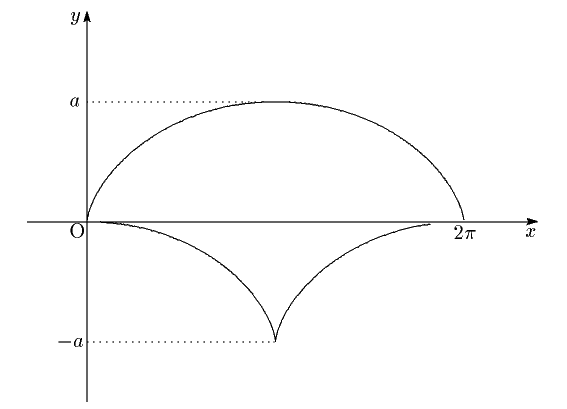
サイクロイド
太郎
他の曲線で,面白いものはありませんか.
南海
サイクロイドの場合,計算ができて,縮閉線が再びサイクロイドになる.
太郎
やってみます.サイクロイドを媒介変数$\theta$と定数$a$によって
\[
f(\theta)=a(\theta-\sin\theta),\ \quad
g(\theta)=a(1-\cos\theta)
\]
とします.
\[
\begin{array}{l}
f'(\theta)=a(1-\cos\theta),\ \quad g'(\theta)=a\sin\theta \\
f''(\theta)=a\sin\theta,\ \quad g''(\theta)=a\cos\theta
\end{array}
\]
なので, $ ① $ , $ ② $ を計算する.$x(\theta)$などは$x$とする.
\[
\begin{array}{l}
(1-\cos\theta)x+(\sin\theta)y=a(1-\cos\theta)\theta\\
(\sin\theta)x+(\cos\theta)y=a(1-\cos\theta+\theta\sin\theta)
\end{array}
\]
となる.
$ 1-\cos\theta\ne 0 $ の下でこれを解くと,
\[
x=a(\theta+\sin\theta),\ \quad
y=a(-1+\cos\theta)
\]
となります.
南海
同じ結果が『解析概論』にある.
そこにあるように,これは再びサイクロイドである.
太郎
引ける法線の数に関する問題はどのようになるのでしょうか.
また『数学対話』の「光の包絡線」に「外サイクロイドと内サイクロイド」があります.
その媒介変数表示は
\[
f(\theta)=(a+b)\cos\theta-b\cos\left(\dfrac{a+b}{b}\theta \right),
g(\theta)=(a+b)\sin\theta-b\sin\left(\dfrac{a+b}{b}\theta \right)
\quad \cdots④
\]
です.これについてもいえるのですか.
南海
これらについては現段階では宿題としておこう.
Aozora
2020-09-5