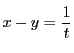 とすると,
とすると,
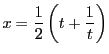 ,
,
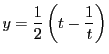 となります.
つまり,
となります.
つまり,
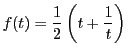 ,
,
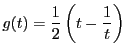 です.
です.
太郎
![]() なので,
なので,![]() ,
,
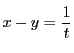 とすると,
とすると,
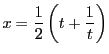 ,
,
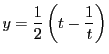 となります.
つまり,
となります.
つまり,
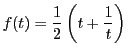 ,
,
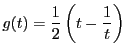 です.
です.
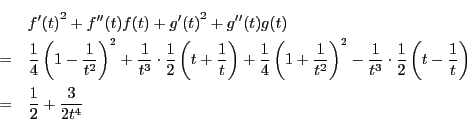
南海 グラフは次のようになる.
太郎
双曲線の媒介変数表示 $ x=f(t),\ y=g(t) $ において,
$ \left(f(t),\ g(t)\right) $ を通る法線上の点 $ (X,\ Y) $ は
\[
X+Y+\dfrac{1}{t^2}(-X+Y)-t+\dfrac{1}{t^3}=0
\]
を満たす.これから
\[
t^4-(X+Y)t^3+(X-Y)t-1=0
\]
となります.
南海
ところがこの形の方程式は大変難しい.
時間をかけて考えてみよう.