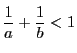 を満たす任意の自然数とするとき,
を満たす任意の自然数とするとき,
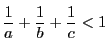 を満たす任意の自然数とするとき,
を満たす任意の自然数とするとき,
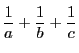 の最大値が
の最大値が
次の問いに答よ.
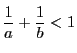 を満たす任意の自然数とするとき,
を満たす任意の自然数とするとき,
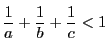 を満たす任意の自然数とするとき,
を満たす任意の自然数とするとき,
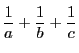 の最大値が
の最大値が
本問の最大値を与える![]() は
は![]() ,
,
![]() ,
,
![]() で得られるものであり,これはよく知られたシルベスター数列の第1,第2,第3項である.この入試問題は,1をエジプト分数で下から近似するとき,最良の近似がシルベスター数列から得られると,一般化される.
で得られるものであり,これはよく知られたシルベスター数列の第1,第2,第3項である.この入試問題は,1をエジプト分数で下から近似するとき,最良の近似がシルベスター数列から得られると,一般化される.
本稿では,さらにそれを一般化して,単位分数をエジプト分数で下から近似するとき,その最良の近似は,拡張された![]() シルベスター数列から得られる,という定理を証明する.そこで用いられる補題は1変数の場合のムーアヘッドの不等式である.
シルベスター数列から得られる,という定理を証明する.そこで用いられる補題は1変数の場合のムーアヘッドの不等式である.