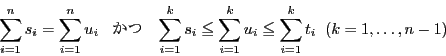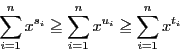次: 一般化定理の証明
上: 単位分数のエジプト分数による下からの近似
前: 一般化定理
次: 一般化定理の証明
上: 単位分数のエジプト分数による下からの近似
前: 一般化定理
次の補題はムーアヘッドの不等式の特別な場合である.
この証明は「対称式と不等式」(文献[3])に教えられたものである.
一般の場合のムーアヘッドの不等式については末尾の文献[2],[3],[4]を参照されたい.
補題 2
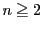
とする.
実数の列
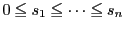
と
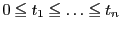
は次の条件,
を満たす.このとき任意の非負実数
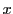
に対し,
不等式
が成立する.
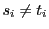
となる
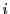
が存在すれば,等号は
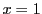
のときのみ成立する.
□
証明
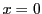 なら明らかなので,
なら明らかなので,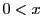 とする.
このときの命題を
とする.
このときの命題を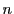 に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
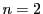 のとき.
のとき.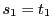 なら
なら
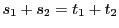 より
より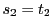 となって等号で成立.
となって等号で成立.
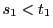 とする.このとき条件から
とする.このとき条件から
である.
と変形される.
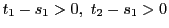 より
より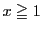 か
か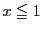 に応じて,
に応じて,
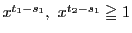 か
か
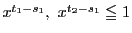 であるから
であるから
となり,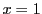 のときにかぎり等号が成立する.よって
のときにかぎり等号が成立する.よって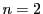 のとき命題は成立する.
のとき命題は成立する.
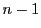 以下のとき,命題が成立するとする.
以下のとき,命題が成立するとする.
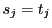 となる
となる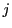 があるとき.
があるとき.
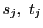 を除く
を除く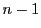 個ずつの
個ずつの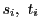 も定理の条件をみたす.
よって数学的帰納法の仮定から,等号成立条件を含め不等式は成立する.
も定理の条件をみたす.
よって数学的帰納法の仮定から,等号成立条件を含め不等式は成立する.
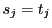 となる
となる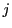 がないとき.
がないとき.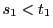 ,
,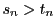 なので,
なので,
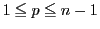 で
で
となる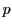 がある.ここで
がある.ここで
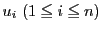 を次のように定義する.
を次のように定義する.
このようにすると
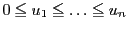 であり,さらに
であり,さらに
が成立する.
ところが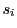 の列と
の列と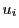 の列,
の列,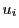 の列と
の列と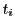 の列にはそれぞれ等しい項がある.
よって,
の列にはそれぞれ等しい項がある.
よって,
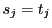 なる
なる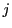 があるときと同様の理由で,数学的帰納法の仮定から
があるときと同様の理由で,数学的帰納法の仮定から
が成立する.これから等号成立条件を含めて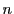 の場合も成立し,
すべての
の場合も成立し,
すべての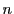 で補題が成立する.
(証明終わり)
で補題が成立する.
(証明終わり)
Aozora
2013-09-03
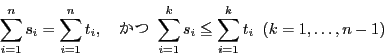
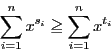
![]() なら明らかなので,
なら明らかなので,![]() とする.
このときの命題を
とする.
このときの命題を![]() に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
![]() のとき.
のとき.![]() なら
なら
![]() より
より![]() となって等号で成立.
となって等号で成立.
![]() とする.このとき条件から
とする.このとき条件から
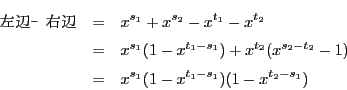
![]() 以下のとき,命題が成立するとする.
以下のとき,命題が成立するとする.
![]() となる
となる![]() があるとき.
があるとき.
![]() を除く
を除く![]() 個ずつの
個ずつの![]() も定理の条件をみたす.
よって数学的帰納法の仮定から,等号成立条件を含め不等式は成立する.
も定理の条件をみたす.
よって数学的帰納法の仮定から,等号成立条件を含め不等式は成立する.
![]() となる
となる![]() がないとき.
がないとき.![]() ,
,![]() なので,
なので,
![]() で
で
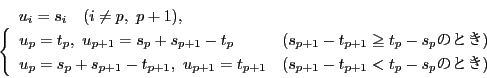
![]() であり,さらに
であり,さらに