それではまず,![]() のとき,つまり
のとき,つまり ![]() を考えよう.
を考えよう.
 図1のように
図1のように ![]() が対角線である正方形の各辺が
が対角線である正方形の各辺が ![]() に区切られ,小正方形
に区切られ,小正方形 ![]() に
分けられている.
に
分けられている.
![]() から
から ![]() への最短経路のうち対角線
への最短経路のうち対角線 ![]() より上半分には出ない
(対角線に乗るところまでは許される)経路の総数を
より上半分には出ない
(対角線に乗るところまでは許される)経路の総数を ![]() とする.ただし
とする.ただし ![]() とする.
とする.
![]() を求める方法は二つある.ひとつは技巧的な工夫をするものだ.
を求める方法は二つある.ひとつは技巧的な工夫をするものだ.
 例 1.2.2
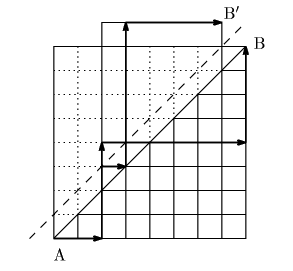
図2を参考にして,
例 1.2.2
図2を参考にして, 解答
不適な場合は必ず対角線を越え出るので, 最初に対角線を越えて到達した点を C とする.
C から AB に平行な向きを対称軸として折り返すと, C から B に至る経路が図の ![]() に至る経路となる. 逆に, A から
に至る経路となる. 逆に, A から ![]() に至る経路を最初に上半分の領域に入った点で逆
に折り戻すことにより, B へ一度は対角線を越えてから至る経路となる. このように, A から B
へ対角線を越えて至る経路と A から
に至る経路を最初に上半分の領域に入った点で逆
に折り戻すことにより, B へ一度は対角線を越えてから至る経路となる. このように, A から B
へ対角線を越えて至る経路と A から ![]() への経路が対応している. したがって, 求める
経路の数は A から B に至るすべての経路の数から上の経路の数を減ずればよい. すなわち,
への経路が対応している. したがって, 求める
経路の数は A から B に至るすべての経路の数から上の経路の数を減ずればよい. すなわち,
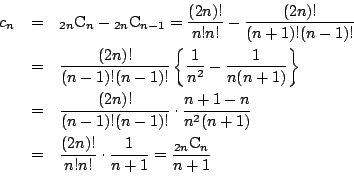
ここで![]() を求めておこう.
を求めておこう.
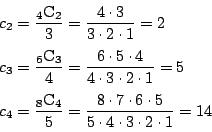
南海 ![]() の漸化式は「生成関数の方法」のなかの
の漸化式は「生成関数の方法」のなかの![]() の漸化式を見てほしい.
の漸化式を見てほしい.
一般的な生成関数による方法がある. これは『数学対話』「生成関数の方法」を見てほしい.