原点 ![]() から出発して座標平面上を
から出発して座標平面上を ![]() 軸の正の方向,または
軸の正の方向,または ![]() 軸の正の方向に1だけ
進むことを次々行って得られる経路を道という.原点と点
軸の正の方向に1だけ
進むことを次々行って得られる経路を道という.原点と点 ![]() を結ぶ,
領域
を結ぶ,
領域
![]() 内の道の総数を
内の道の総数を ![]() とする.次の問に答えよ.
とする.次の問に答えよ.
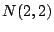 ,
, 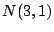 ,
, 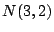 を求めよ.
を求めよ.
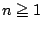 のとき,
のとき, 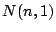 を求めよ.
を求めよ.
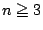 のとき,
のとき, 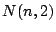 を
を 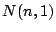 と
と 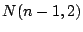 で表し
で表し
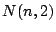 を求めよ.
を求めよ.
原点 ![]() から出発して座標平面上を
から出発して座標平面上を ![]() 軸の正の方向,または
軸の正の方向,または ![]() 軸の正の方向に1だけ
進むことを次々行って得られる経路を道という.原点と点
軸の正の方向に1だけ
進むことを次々行って得られる経路を道という.原点と点 ![]() を結ぶ,
領域
を結ぶ,
領域
![]() 内の道の総数を
内の道の総数を ![]() とする.次の問に答えよ.
とする.次の問に答えよ.
南海 これは解けたのかな.
耕一 はい.解は
それで質問は,
この ![]() は一般に求まるのか,またこの
は一般に求まるのか,またこの ![]() にはどんな意味があるのか,
ということです.
にはどんな意味があるのか,
ということです.