


次: 生成関数による別解
上: 生成関数の方法
前: 二つの入試問題
南海 実は青空学園ではすでにいちど生成関数を使って入試問題の一般化を解いている.
98年の京大の入試問題の一般化だ.これを後で紹介しよう.
ここで少し生成関数についてまとめよう.
数列
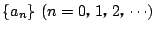 がある.
がある. 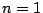 から始まるときは
から始まるときは 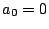 とすればよい.
有限数列なら,あるところから先の項はすべて 0 とすれば,
有限,無限数列関係なく考えられる.
この数列に対して, 各項
とすればよい.
有限数列なら,あるところから先の項はすべて 0 とすれば,
有限,無限数列関係なく考えられる.
この数列に対して, 各項 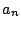 を係数とする無限級数
を係数とする無限級数
を考え,これを数列の「生成関数」と呼ぶことにする.
これは無限級数なので収束しなければ「関数」とはいえない.
十分小さい 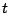 で
で
が成り立てば,
がいえる.
生成関数を考えその関係式から係数の関係を導くためには,
収束半径が 0 でさえなければよい.
したがってひとつひとつの関数について収束する
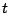 の範囲を考える必要はない.
の範囲を考える必要はない.
二つの生成関数
に対して
となる.
-
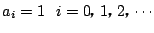 のとき.
のとき.
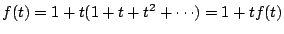 なので,
なので,
-
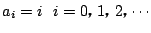 のとき.
のとき.
ゆえに
-
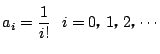 のとき.
のとき.
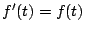 なので
なので
この生成関数の方法は,実に強力なものだ.漸化式を解くのにも役立つ.漸化式が与えられると,
それに対応して f(t) の関係式が得られる. それをもとに, f(t) の級数展開の一般項をつくれば,
それによって係数の一般項が得られる.三項間漸化式を生成関数で解く方法などもまた説明しよう.
Aozora Gakuen
![]() がある.
がある. ![]() から始まるときは
から始まるときは ![]() とすればよい.
有限数列なら,あるところから先の項はすべて 0 とすれば,
有限,無限数列関係なく考えられる.
この数列に対して, 各項
とすればよい.
有限数列なら,あるところから先の項はすべて 0 とすれば,
有限,無限数列関係なく考えられる.
この数列に対して, 各項 ![]() を係数とする無限級数
を係数とする無限級数
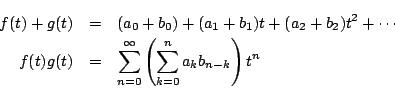
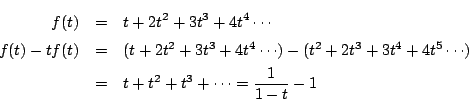
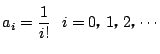 のとき.
のとき.