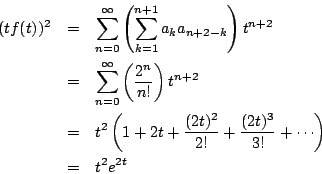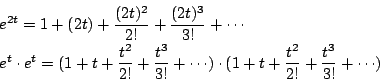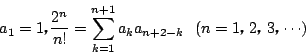次: カタラン数を生成関数で求める
上: 生成関数の方法
前: 生成関数
耕一 それでは解いてみます.
解答[横国大の別解]
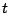 の無限級数を
の無限級数を
とおく.ここで,
よって
つまり
である.よって
これが
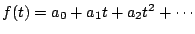 と一致するので
と一致するので
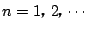 に対して
に対して
□
解答[北大の別解]
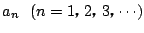 に対して
に対して
とおく.
である.
ところが 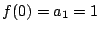 より
より 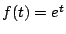
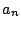 は
は 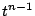 の係数なので
の係数なので
□
南海 ずいぶん簡明に,見通しよく解けるだろう.
ただ注意すべきは,たとえば北大の問題の別解だが,これはなにも本質的に新しい解法ではない.
耕一 といいますと….
南海 実は
この二式が形式的無限級数として一致することを示そうとすると結局
に対して
を示さねばならないのだ.
生成関数は数列を統一してひとつの関数として扱う方法だ,ということである.
Aozora Gakuen
![]() の無限級数を
の無限級数を
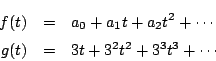
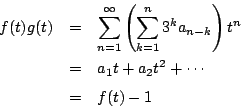
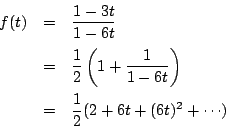
![]() に対して
に対して