関数
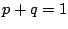 を満たす任意の正の数
を満たす任意の正の数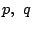 と,関数の定義域の任意の
と,関数の定義域の任意の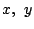 に対して,
に対して,
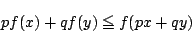
が成り立つことを平均値の定理を用いて示せ.-
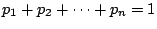 を満たす任意の正の数
を満たす任意の正の数
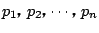 と,
定義域内の任意の実数
と,
定義域内の任意の実数
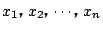 に対して
に対して
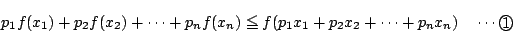
が成り立つことを示せ. 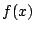 として適切な関数を選ぶことにより
として適切な関数を選ぶことにより
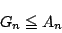
を示し,等号が成立する場合を述べよ.
まずはもっとも一般的な凸関数を使うものである. (2)の部分は98年大阪市立大学後期試験に出題されている.
![]() とする.このとき
とする.このとき ![]() である.
である.
区間 ![]() で平均値の定理を用いると,
で平均値の定理を用いると,
![]() で
で
同様に区間 ![]() で平均値の定理を用いると,
で平均値の定理を用いると,
![]() で
で
![]() のときは(1)から成立.
のときは(1)から成立.
![]() 個の場合に成立するとし
個の場合に成立するとし ![]() 個の場合に成立することを示す.
個の場合に成立することを示す.
![]() とおく.
とおく.
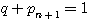 であることに注意する.
であることに注意する.
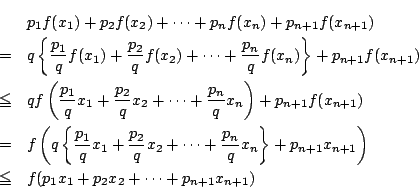
よって一般の ![]() に対して題意が示された.
に対して題意が示された.
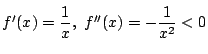 である.
である.
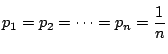 で(2)の結果を用いる.
で(2)の結果を用いる.
注意 これからただちに次の不等式も成立する.
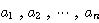 と
と 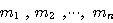 を正の実数とする.
を正の実数とする.
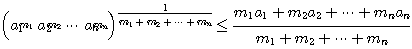
左辺右辺それぞれ,重みつき相乗平均,重みつき相加平均という.
方法 2 (1の別証)
関数 ![]() が2回微分可能で
が2回微分可能で![]() を満たしているとする.
定義域内の任意の
を満たしているとする.
定義域内の任意の![]() に対して
に対して
これを
![]() および
および
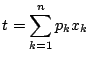 で用いることにより1を示せ.
で用いることにより1を示せ.
つまり,定義域内の任意の![]() に対して
に対して
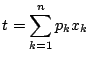 として,
として,
![]() に
に![]() を代入し,
を代入し,
![]() をかけて
をかけて
![]() について加える.
について加える.
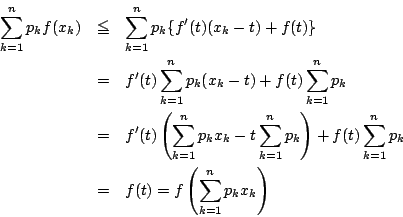
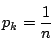 で
示せばよい.これは96年京都教育大学で出題されている.
で
示せばよい.これは96年京都教育大学で出題されている.
この方法の優れているところは, 数学的帰納法を使うことなく示せることである. 相加平均,相乗平均の不等式を導くために1の形まで示すのは,そうしないと帰納法ができないからである.