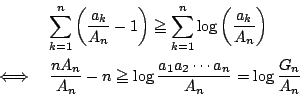[79鹿児島大]
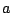 を与えられた正の定数とするとき,
を与えられた正の定数とするとき,
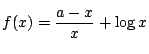 の最小値を求めよ.
ただし,
の最小値を求めよ.
ただし, 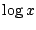 は
は 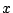 の自然対数を表すものとする.
の自然対数を表すものとする.
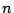 個の関数
個の関数
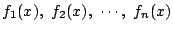 と
それらの和
と
それらの和
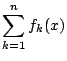 がいずれも最小値をもつとき,それらの最小値を,それぞれ,
がいずれも最小値をもつとき,それらの最小値を,それぞれ,
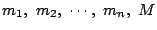 とすると,
とすると,
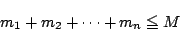
となることを示せ.- 上の結果を利用して
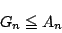
を示せ.また,この不等式で等号が成立する場合を吟味せよ.
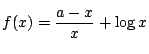 の最小値を求めよ.
ただし,
の最小値を求めよ.
ただし, 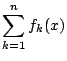 がいずれも最小値をもつとき,それらの最小値を,それぞれ,
がいずれも最小値をもつとき,それらの最小値を,それぞれ,
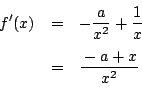
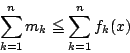
一方,和
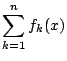 が
が
![]() で最小値
で最小値![]() をとるとすると,
をとるとすると,
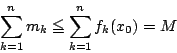
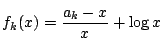 とおく.
これは
とおく.
これは
一方
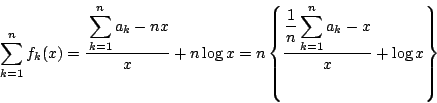
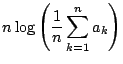 である.したがって(1)から
である.したがって(1)から
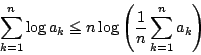
また別のものが 00年滋賀県立大で出題された. 昔から知られている方法である.
解
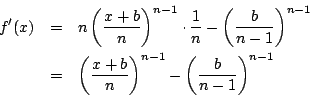
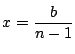 で極小かつ最小である.
つまり
で極小かつ最小である.
つまり
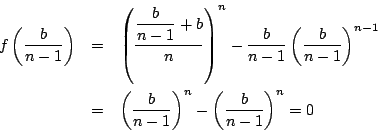
![]() のときより
のときより![]() が正の実数で
が正の実数で
![]() が2以上の自然数のとき,不等式
が2以上の自然数のとき,不等式
![]() のとき(1)の結論から
のとき(1)の結論から
![]() で成立するとする.
で成立するとする.
![]() ,
,
![]() ,
,
![]() で(1)の結論を用いると
で(1)の結論を用いると
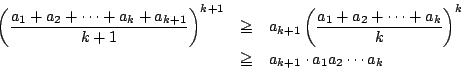
したがって ![]() の自然数について
の自然数について
これと同じ問題が,形を変えて出題されている.これは例題として掲げておく.
方法4で,bをAに,aをxに,nをn+1にすれば同じである.
例題 [05徳島大]
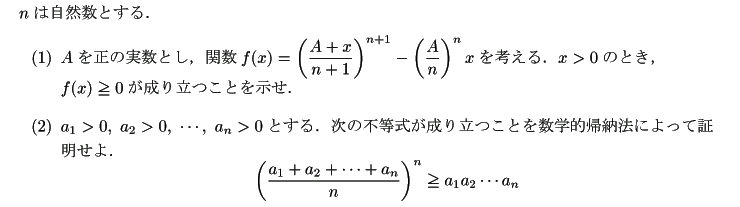
多項式関数を用いる方法としては,次のものが標準的である.
解
![\begin{eqnarray*}
{f_n}'(x)
&=&\dfrac{1}{n}-\sqrt[n]{A}\cdot
\dfrac{1}{n}x^{ ...
...{n}-1}\\
&=&\dfrac{1}{n}(1-A^{ \frac{1}{n}}x^{\frac{1-n}{n}})
\end{eqnarray*}](images/img111.png)
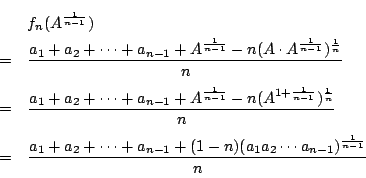
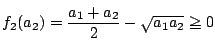 .
つまり
.
つまり
(1)の最小値を ![]() で用いて
で用いて
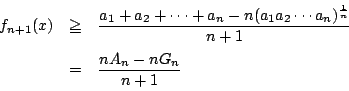
次のものは凸関数を用いる証明[2]と本質的には同じなのだが, 相加平均,相乗平均の大小関係の証明に特化することでより簡単にできる. 二つの方法をまとめてある.雜誌『初等数学』(1999年8月号)の宮地俊彦先生の報告による.
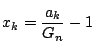 とおけ.得られた不等式を
すべて加えることで
とおけ.得られた不等式を
すべて加えることで
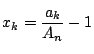 とおけ.得られた不等式を
すべて加えることで
とおけ.得られた不等式を
すべて加えることで
解
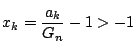 である. (1)から
である. (1)から
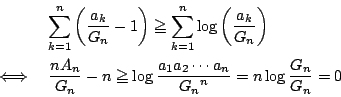
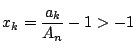 なので(1)が使える.
なので(1)が使える.