次: ベクトル空間の基底 上: ベクトル空間と線型写像 前: 一次変換から線型写像へ

ベクトル空間と線型写像の定義

南海　 行列を間にはさんで得られた $f(k\overrightarrow{u})=kf(\overrightarrow{u})$のような関係は， 写像$f$が行列を用いて定義されているということとは独立な $f$自身の性質である． そこで，平面や空間の矢線，また行列から離れて，次のようにベクトル空間と線型写像を定義しよう．

耕一　 いったん行列から離れるのですか．

南海　 ベクトルとは必ずしも矢線ではない． 行列は線型写像に固有のものではない． 後で見るように，同じ線型写像でもいろんな行列表現をもつ． 行列と線型写像を切り離して考えることができないと， 行列の対角化の意味もわかりづらい． そこでベクトルの記号だが，矢線をつけて $\overrightarrow{u}$ と表す代わりに，書体を変えて， $\mathrm{\bf u}$と表すことにする．

定義 1 (ベクトル空間)
ベクトルの集合$V$が次の性質をもつとき， $V$をベクトル空間という．

(i)

和が定まり，交換法則

$$\mathrm{\bf u}+\mathrm{\bf v}=\mathrm{\bf v}+\mathrm{\bf u}$$

と，結合法則

$$\mathrm{\bf u}+(\mathrm{\bf v}+\mathrm{\bf z}) =(\mathrm{\bf u}+\mathrm{\bf v})+\mathrm{\bf z}$$

が成り立つ．

任意のベクトル $\mathrm{\bf u}$に対して

$$\mathrm{\bf u}+\mathrm{\bf e}=\mathrm{\bf u}$$

となるベクトル $\mathrm{\bf e}$が存在する． これを零ベクトルといい，$\mathrm{\bf0}$と表す．

任意のベクトル $\mathrm{\bf u}$に対して

$$\mathrm{\bf u}+\mathrm{\bf v}=\mathrm{\bf0}$$

となるベクトル $\mathrm{\bf v}$が存在する． これをベクトル $\mathrm{\bf u}$の逆ベクトルといい， $-\mathrm{\bf u}$と表す．

言いかえると，$V$は加法に関して可換な群である．

(ii)

実数倍 $k\mathrm{\bf u}$が定義され， 実数$k,\ l$に対し

$$\begin{array}{l} 1\mathrm{\bf u}=\mathrm{\bf u}\\ k\left... ...+l)\mathrm{\bf u}=k\mathrm{\bf u}+l\mathrm{\bf u} \end{array}$$

が成り立つ．また和との間に分配法則

$$k(\mathrm{\bf u}+\mathrm{\bf v}) =k\mathrm{\bf u}+k\mathrm{\bf v}$$

が成り立つ．

定義 2 (線型写像)
ベクトル空間$V$からベクトル空間$W$への写像$f$が次の性質をもつとき， $f$を線型写像という． 任意のベクトル $\mathrm{\bf u},\ \mathrm{\bf v}$と実数$k$に対して

$$\begin{array}{l} f(k\mathrm{\bf u})=kf(\mathrm{\bf u})\\ ... ...thrm{\bf v}) =f(\mathrm{\bf u})+f(\mathrm{\bf v}) \end{array}$$

をみたす．

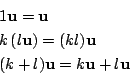
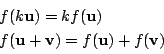
これをベクトル空間と線型写像の定義としよう． 定義するとは，考える対象を明確にすることだ． このように考える対象をはっきりさせることが，数学では大切なのだ． ベクトルを「方向と大きさのある数学的対象」と 考えるかぎり見えてこないが， 上のように定義することで，次のような対象もベクトル空間となる．

例 1.2.1  

1. 漸化式
   
   $$a_{n+2}+pa_{n+1}+qa_n=0$$
   
   
   を満たす数列$\{a_n\}$の集合．
   
   $$V=\{\ \{a_n\}\ \vert\ a_{n+2}+pa_{n+1}+qa_n=0\ \}$$
   
   
   実際，$V$の2つの要素 $\{a_n \},\ \{b_n \}$と 任意の定数 $\alpha,\ \beta$に対して
   
   $$c_n=\alpha a_n+\beta b_n$$
   
   
   で数列$\{ c_n \}$を定めると，$\{ c_n \}$も同じ漸化式を満たす． これから$V$がベクトル空間であることがわかる．
2. 微分方程式
   
   $$\dfrac{d^2}{dx^2}f(x)+p(x)\dfrac{d}{dx}f(x)+q(x)f(x)=0$$
   
   
   を満たす関数$f(x)$の集合$V$． これも $V$の2つの要素$f(x),\ g(x)$と任意の定数 $\alpha,\ \beta$に対して
   
   $$h(x)=\alpha f(x)+\beta g(x)$$
   
   
   で関数$h(x)$を定めると，$h(x)$も同じ微分方程式を満たす． これから$V$がベクトル空間であることがわかる．

数学ではこのように，考えている対象の本質を取り出すことで， 他の分野のある対象も同じ本質を満たすことがわかり， 視野が広がることがよくある． 今は一般的に「本質」といったが，数学的にいえば「構造」ということだ． 平面ベクトルの集合と， 漸化式を満たす数列の集合が「同じ構造をもつ」ということだ．

耕一　 ベクトルは「向き」と「大きさ」からなる数学の対象だと習いました． 確かに上の例はそれではとらえられない対象です． では逆に， 一般的なベクトル空間に大きさの概念はどのように定義されるのでしょうか． また高校では，2次元の平面ベクトルと3次元の空間ベクトルという風に 別々に分けて習いました．これまでのところ，ベクトル空間の定義には次元の概念もありません．

南海　 上のベクトル空間の定義には，まだ大きさは定義されていない． 「大きさ」の概念なしにどのようなことまでが成り立つのかを考えるのだ． 「線型代数」の 一般的な教程ではベクトルの大きさや距離は後で導入される． 後ほどベクトルの「大きさ」も定義しよう． また，次元は先に定義されていることではなく，次に考えるように， このベクトル空間の定義のなかから，ベクトル空間に固有の値として， 次元の概念がうかびあがってくる．