ベクトル空間
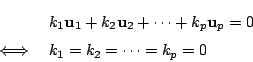
が成り立つとき,
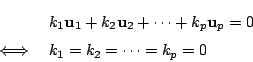
![]() が一次独立であることは,
が一次独立であることは,
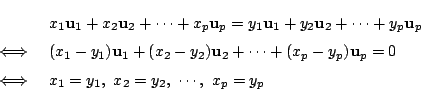
さて,ベクトル空間![]() の
の![]() 個のベクトル
個のベクトル
![]() は一次独立で,さらに,
は一次独立で,さらに,
![]() に,これらと異なる0ベクトルでない
に,これらと異なる0ベクトルでない![]() のベクトル
のベクトル
![]() をどのように選んで加えても,
それを加えた
をどのように選んで加えても,
それを加えた
![]() はもはや一次独立ではないとき,
はもはや一次独立ではないとき,
![]() は
は![]() の
最大独立系をなすという.
の
最大独立系をなすという.
定義から最大独立系に属するベクトルは零ベクトルではない.
![]() が最大独立系のとき,
が最大独立系のとき,![]() の任意のベクトル
の任意のベクトル
![]() に対し実数
に対し実数
![]() を選んで,
を選んで,
$ \mathrm{u_1,\ u_2,\ \cdots,\ u_p}$
$ \mathrm{v_1,\ v_2,\ \cdots,\ v_q}$
証明
![]() とし,
とし,![]() とする.
とする.
![]() は
は
$ \mathrm{u_1}=a_1\mathrm{v_1}+a_2\mathrm{v_2}+\cdots+a_q\mathrm{v_q}$
$ \mathrm{u_1,\ v_2,\ \cdots,\ v_q}$
![]() に,
に,
![]() を
$ \mathrm{u_1,\ v_2,\ \cdots,\ u_q} $
で表したものを代入することにより,
を
$ \mathrm{u_1,\ v_2,\ \cdots,\ u_q} $
で表したものを代入することにより,![]() の任意のベクトルが,
$ \mathrm{u}_1,\ \mathrm{v}_2,\ \cdots,\ \mathrm{u}_q$
で表される.
よって特に
の任意のベクトルが,
$ \mathrm{u}_1,\ \mathrm{v}_2,\ \cdots,\ \mathrm{u}_q$
で表される.
よって特に
![]() が
が
$\mathrm{u_2}= b_1\mathrm{u_1}+b_2\mathrm{v_2}+\cdots+b_q\mathrm{v_q}$
$\mathrm{u_1},\ \mathrm{u_2},\ \mathrm{v_3},\ \cdots,\ \mathrm{v_q}$
$\mathrm{v_1,\ v_2,\ \cdots,\ v_q}$
したがって![]() ではあり得ない.
つまり
ではあり得ない.
つまり![]() であることが示された.□
であることが示された.□
耕一 そうか.わかった.ベクトル空間の次元とは, 最大独立系のベクトルの個数なのです. 平面ベクトルでは2個の一次独立なベクトルがとれ, 空間ベクトルでは3個の一次独立なベクトルがとれる.
南海 次元の定義はいろいろある.しかし実数体上のベクトル空間に関して言えば, いま言ったとおり最大独立系をなすベクトルの個数と考えてよい.
耕一 では大きさは?