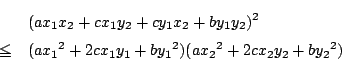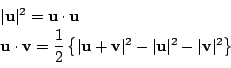
耕一
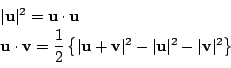
南海 そこで,内積が先か,大きさが先かということになる. 結論的には,ベクトル空間は内積を基礎にする.
耕一
『数学対話』-「高校数学の土台」-「座標の方法」-「ベクトルと座標」では,
内積の2つの定義
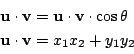
南海
今は,それ以前の議論をしている.
第1の定義のなかで用いられている「大きさ」と,
「なす角![]() 」はどのように定めるのか.
また,第2の定義で用いた座標は,ベクトル空間
」はどのように定めるのか.
また,第2の定義で用いた座標は,ベクトル空間![]() では,
まだ設定されていない.
では,
まだ設定されていない.
耕一 確かに.
南海
ベクトル空間![]() の内積を,次のように定義しよう.
の内積を,次のように定義しよう.
第3の条件は,内積の定義そのものには不要で,
この条件を満たすものを特に「正値な内積」と呼ぶのだが,
簡単のためここではこの条件も内積の定義のなかに入れておく.
直交座標が定まっていて,大きさが普通のユークリッド式の距離であるときは,
![]() を
を
![]() と書くのだった.
と書くのだった.
耕一
![]() は何から来ているのですか.
は何から来ているのですか.
南海
性質(i)と(ii)は,
![]() が,
が,
![]() のそれぞれについて
一次(線型)であるということを意味している.
すなわち
のそれぞれについて
一次(線型)であるということを意味している.
すなわち
![]() を固定し,
を固定し,
![]() を変数とすると,
を変数とすると,
![]() は
は![]() から実数への線型写像になっている.
逆に
から実数への線型写像になっている.
逆に
![]() を固定しても同様である.
つまり内積は双線型(bilinear)なのだ.この
を固定しても同様である.
つまり内積は双線型(bilinear)なのだ.この![]() から来ている.
から来ている.
さて,今はまだ座標も定まっていない段階だが,
普通の![]() 座標が入った平面ベクトルでの内積の例を作っておこう.
座標が入った平面ベクトルでの内積の例を作っておこう.
耕一 内積の満たすべき性質(i)から
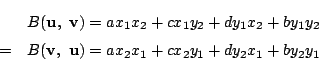
以上から
南海
そう.
さて,この内積を用いて,
ベクトルの大きさとしての絶対値
![]() を次のように定める.
を次のように定める.
![]() によって定まる絶対値という意味で
によって定まる絶対値という意味で![]() を添えて書いておこう.
を添えて書いておこう.
耕一
これは内積の定義から
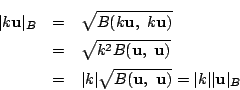
南海
問題は三角不等式だ.つまり内積とそれを用いた絶対値の定義に対し
耕一 両辺負ではないので,2乗する. 左辺の2乗は
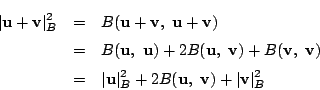
南海
実はこれより強い
耕一
これって,普通の場合,成分で書くと
南海 そう.この不等式が一般的な内積で成立する.これを証明しよう.
証明
![]() のときは両辺0で成立.
のときは両辺0で成立.
![]() とする.
内積の定義(iii)から,任意の実数
とする.
内積の定義(iii)から,任意の実数![]() に対して
に対して
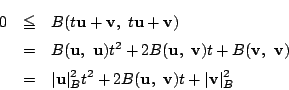
耕一 ということは先の例で考えた内積でこれを実際に書くと