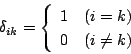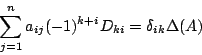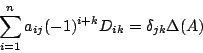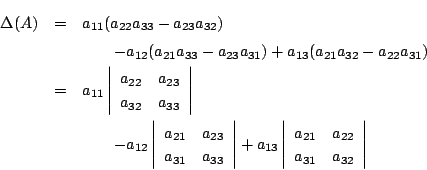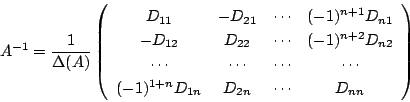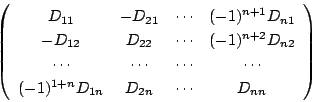次: クラメルの公式
上: 行列と行列式
前: 行列式の定義
南海
行列式の定義そのままではいろんな応用に不便である.
なぜこれが逆行列の構成に役立つのかもみにくい.
これに対して,行列式を余因子といわれる小行列式を用いて展開し計算することができる.
行列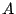 のあるひとつの要素
のあるひとつの要素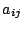 とする.
とする.
の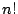 個の項のうち,
個の項のうち,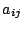 を因子にもつものをまとめ,
そこから
を因子にもつものをまとめ,
そこから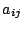 をくくりだして,これを
をくくりだして,これを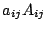 と書こう.
行列式のすべての項は第
と書こう.
行列式のすべての項は第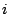 行の要素を1つ,そしてただ1つだけ含んでいる.
だから行列
行の要素を1つ,そしてただ1つだけ含んでいる.
だから行列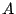 の
の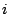 行をとって
行をとって
と表せる.これを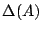 の
の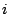 行目の要素による展開という.
同様に
行目の要素による展開という.
同様に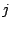 列をまとめて部分和をつくることによって,
列をまとめて部分和をつくることによって,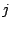 列目の要素による次の展開が得られる.
列目の要素による次の展開が得られる.
耕一
3次行列で確認します.
( )内も行列のようです.
南海
そこで,係数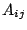 がどんなものであるかを調べよう.
要素
がどんなものであるかを調べよう.
要素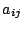 を含む項はすべて次の形をしている.
つまり
を含む項はすべて次の形をしている.
つまり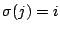 となる置換で
となる置換で
これらから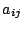 を除いたものは,符号を別にして,
もとの行列から
を除いたものは,符号を別にして,
もとの行列から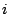 行と
行と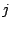 列の要素をすべて取り除いて得られた小行列式の項である.
列の要素をすべて取り除いて得られた小行列式の項である.
に対し
とおこう.
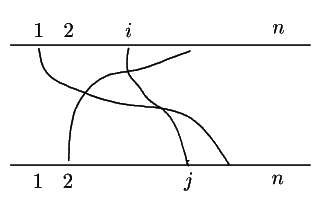
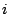 と
と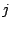 を結ぶひもと交わるひもで,左から右に交わるものを
を結ぶひもと交わるひもで,左から右に交わるものを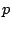 本,
右から左に交わるもの
本,
右から左に交わるもの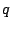 本とすれば
本とすれば
である.よってその和は
である.
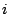 と
と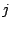 を取りのぞいた交点数の偶奇で
を取りのぞいた交点数の偶奇で
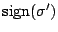 が決まるので
が決まるので
が成り立つ.
これがすべての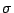 で成立する.
ゆえに
で成立する.
ゆえに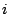 行と
行と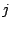 列の要素をすべて取り除いて得られた行列の行列式を
列の要素をすべて取り除いて得られた行列の行列式を
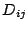 とすると,
とすると,
が成り立つ.つまり
という展開が成り立つ.
また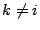 のとき
のとき
である.
これは,元に戻せばはじめの行列式の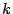 行目をすっかり
行目をすっかり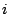 行目に置きかえたものになり,
2つの行が一致する行列の行列式そのものだからである.
行目に置きかえたものになり,
2つの行が一致する行列の行列式そのものだからである.
便利な記号として
とおくと
が成り立つ.
同様に
も成り立つ.
耕一
3次行列で確認します.
です.
これで逆行列も作れます.
なので
です.
南海
ということだ.いま作った行列
のことを,もとの行列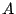 の余因子行列という.
の余因子行列という.
誤植:行列のD2nに(-1)2+nが抜けています.



次: クラメルの公式
上: 行列と行列式
前: 行列式の定義
Aozora Gakuen
![]() のあるひとつの要素
のあるひとつの要素![]() とする.
とする.
![]() がどんなものであるかを調べよう.
要素
がどんなものであるかを調べよう.
要素![]() を含む項はすべて次の形をしている.
つまり
を含む項はすべて次の形をしている.
つまり![]() となる置換で
となる置換で
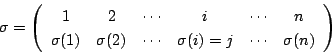
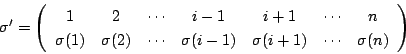

![]() と
と![]() を取りのぞいた交点数の偶奇で
を取りのぞいた交点数の偶奇で
![]() が決まるので
が決まるので