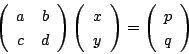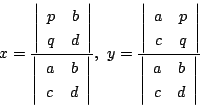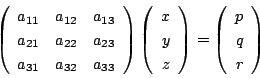次: 固有ベクトルと線型写像の対角表現
上: 行列と行列式
前: 行列式の展開
南海
連立方程式の解公式であるクラメルの公式を作っておこう.
連立方程式は
と表されるものであった.
これは行列では
と表せる.したがって
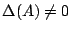 のときは,ただ一組の解
のときは,ただ一組の解
が定まる.
ところが
なので
ただし,最後の行列式は,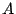 の第
の第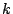 列
列
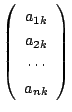 を
を
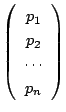 に置きかえたものである.
に置きかえたものである.
耕一
2次と3次では次のようになる.
演習 9
解答
9
次の等式を証明せよ.またその一般化を考えよ.
-
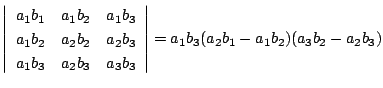
-
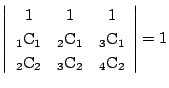
-
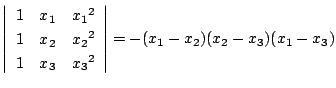
Aozora Gakuen
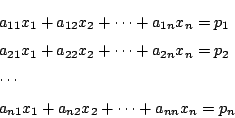
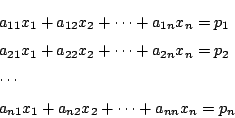
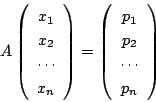

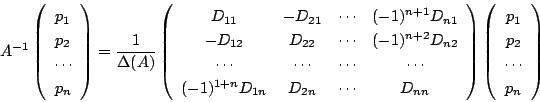
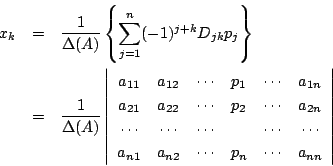
 を
を
 に置きかえたものである.
に置きかえたものである.