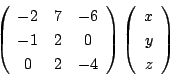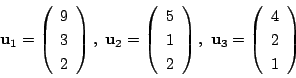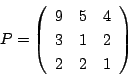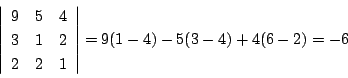次: ハミルトン・ケイレイの定理
上: 固有ベクトルと線型写像の対角表現
前: 固有値と固有ベクトル
南海 定理 5 によって,
もし固有方程式が0でない相異なる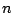 個の根をもつなら,
個の根をもつなら,
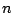 個の一次独立な固有ベクトルが得られる.
個の一次独立な固有ベクトルが得られる.
それらのベクトルを基底として線型写像を表現すれば,
その行列は対角行列である.
『一次変換を見る』にいろんな例を作ってみた.参考にしてほしい.
耕一
『一次変換を見る』の最初の例を,詳しく見てみます.
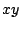 平面で
平面で
を基底とするとき,
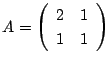 で表される線型写像が
で表される線型写像が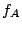 です.
です.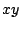 平面の格子点と
平面の格子点と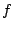 による行き先を結ぶと,2つの方向が見て取れます.
による行き先を結ぶと,2つの方向が見て取れます.
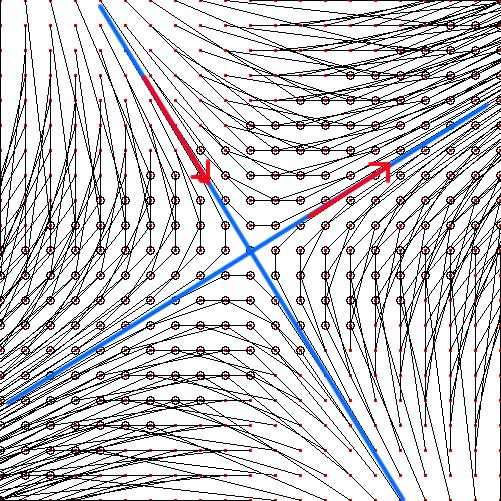
この方向が固有ベクトルの方向です.
固有方程式は
これを解いて
です.この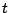 に対して
に対して
です.
固有ベクトルを
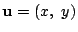 とすると,
とすると,
です.これから固有ベクトルによる基底として
がとれます.すると
となり,
とおけば
となるはずです.実際
なので
です.
南海
固有方程式が重根をもつ場合,対角化はできるのか,
あるいはできないならどのような標準形に変換できるのかという問題などは,
後に考えよう.
次に3次行列
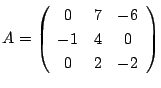 を対角化してみてほしい.
を対角化してみてほしい.
耕一
これを解いて
となる.
それぞれの固有値に対する固有ベクトルを求める.
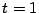 のとき.
のとき.
を解いて,
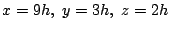 と任意の数
と任意の数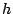 を用いて表せる.
を用いて表せる.
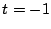 のとき.
のとき.
を解いて,
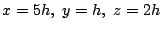 と任意の数
と任意の数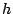 を用いて表せる.
を用いて表せる.
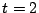 のとき.
のとき.
を解いて,
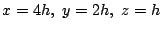 と任意の数
と任意の数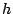 を用いて表せる.
を用いて表せる.
したがって3つの固有ベクトルは
となる.
2次の場合と同様に
とおくと,
これから
そして確かに
となります.



次: ハミルトン・ケイレイの定理
上: 固有ベクトルと線型写像の対角表現
前: 固有値と固有ベクトル
Aozora Gakuen
![]() 平面で
平面で
 で表される線型写像が
で表される線型写像が
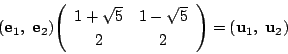
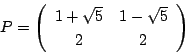
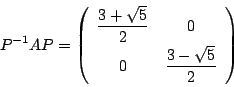
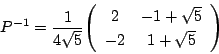
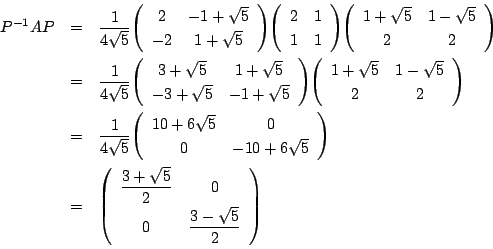
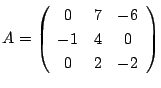 を対角化してみてほしい.
を対角化してみてほしい.
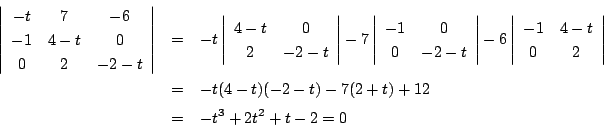
![]() のとき.
のとき.
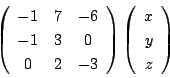
![]() のとき.
のとき.
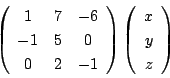
![]() のとき.
のとき.