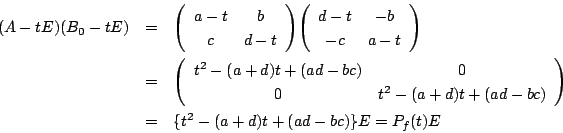次: ジョルダンの標準形
上: 固有ベクトルと線型写像の対角表現
前: 行列の対角化
南海
ハミルトン・ケイレイの定理は高校数学Cにも載っている.
耕一
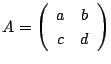 のとき
のとき
です.
この式は固有方程式そのものです.
南海
いいところに気づいた.実は次の事実が成り立つ.
定理 6 (ハミルトン・ケイレイの定理)
を線型写像とし,ある基底で
が行列
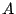
で表されたとする.
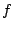
の固有多項式を
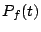
とすると
証明
とおく.
また,行列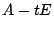 の余因子行列を
の余因子行列を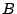 とおく.
とおく.
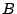 の各成分は
の各成分は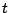 の
の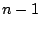 次以下の多項式である.
次以下の多項式である.
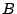 の各成分の
の各成分の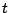 の
の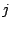 次の項の係数を成分とする行列を
次の項の係数を成分とする行列を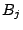 とおくと
とおくと
と書ける.
行列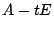 の余因子行列が
の余因子行列が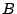 なので,第3節の等式 (1.2) より
なので,第3節の等式 (1.2) より
これから
を得る.
なので,
これが任意の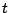 で成立するので,
で成立するので,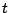 の各次数の行列の各成分が両辺一致する.つまり,
の各次数の行列の各成分が両辺一致する.つまり,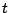 の各次数の行列が一致する.
の各次数の行列が一致する.
第1式の両辺に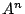 を,第2式の両辺に
を,第2式の両辺に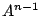 を左から乗じ,以下同様にすると.
右辺は数と
を左から乗じ,以下同様にすると.
右辺は数と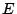 の積なので
の積なので
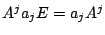 等が成り立つ.よって
等が成り立つ.よって
これをすべて加えると
を得る.□
耕一
2次行列のときに確認してみます.
前と同様に直交座標の 軸
軸 軸方向の単位ベクトルを基底にして
軸方向の単位ベクトルを基底にして
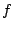 が
が
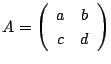 で表されるとします.
で表されるとします.
です.ここで行列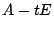 は
は
なので,その因子行列は
です.
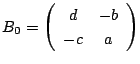 とします.
とします.
そうか.
要するに
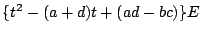 が
が
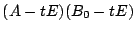 と因数分解されるのですね.
と因数分解されるのですね.
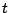 に
に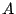 を代入すると
を代入すると
です.
教科書では単なる計算として書かれていますが,
この余因子を作る方法の方が納得できます.
南海
一般の場合も積の順序の問題を明確にするため,
いったん分けてから代入して加えたが,
因数分解できている行列の式に代入したことに変わりない.
演習 10
解答
10
次の行列の最小多項式を求め,
各行列の8乗を計算せよ.
Aozora Gakuen
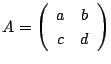 のとき
のとき
 のとき
のとき
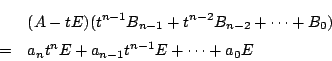
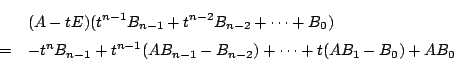
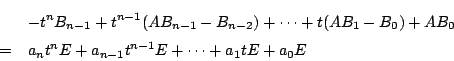
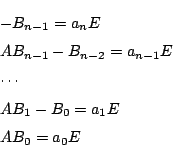
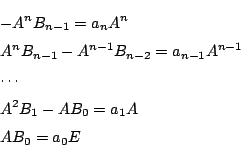
![]() 軸
軸![]() 軸方向の単位ベクトルを基底にして
軸方向の単位ベクトルを基底にして
![]() が
が
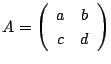 で表されるとします.
で表されるとします.
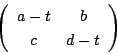
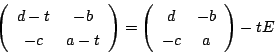
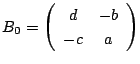 とします.
とします.