


次: 固有値の方法
上: 三項間漸化式と行列の累乗
前: 三項間漸化式と連立漸化式
ではこれをもとに三項間漸化式を行列で求めよう.
三項間漸化式1に対し,連立二項間漸化式5を作る.
5の行列を
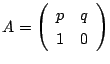 とする.
とする.
であるから,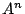 が求まればよい.
行列の
が求まればよい.
行列の 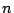 乗を求める方法はいろいろある.最も簡単で便利な方法を用いよう.
乗を求める方法はいろいろある.最も簡単で便利な方法を用いよう.
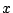 を変数として
を変数として
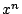 を
を
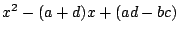 で割った余りを
で割った余りを 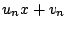 とする.つまり
とする.つまり
と表される.このとき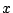 の所に
の所に 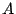 を代入すれば
を代入すれば
となる.
したがって
あとは 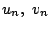 を決めればよい.
を決めればよい.
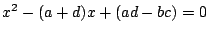 の2解を
の2解を
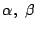 とする.つまり
とする.つまり
とする.
(1)
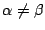 のとき.
のとき.
より
(2) 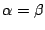 のとき.
のとき.
であるから
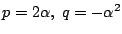 .よって
.よって
であることに注意する.さて
の両辺を微分する.
それぞれに 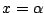 を代入する.
を代入する.
南海 これで三項間漸化式が解けたのだが,行列を使わない解法もまとめておこう.
拓生 はい.
三項間漸化式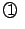 に対して,二次方程式
に対して,二次方程式
をこの三項間漸化式の特性方程式という.
特性方程式の解を
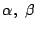 とする.
とする.
である.つまり三項間漸化式は
と表される.
-
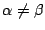 のとき
のとき
と変形できる.ゆえに
この辺々を引けば
これから
これはもちろん と同一の結果である.
と同一の結果である.
-
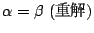 のとき
のとき
つまり
したがって
ゆえに
南海 上で求めた 数列 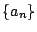 の一般項を少し違う立場で考えよう.
2数
の一般項を少し違う立場で考えよう.
2数 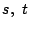 と
二つの数列
と
二つの数列
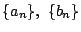 に対して数列
に対して数列 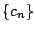 を
を
で定めこれを
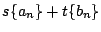 と書く.つまり
と書く.つまり
と定める. 数列 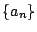 と 数列
と 数列 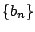 がともに漸化式
がともに漸化式
を満たすとき
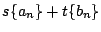 も同じ漸化式を満たす.
実際
も同じ漸化式を満たす.
実際
だからである.
そこで 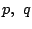 を実数の定数とし,一つの漸化式を満たす数列の集合を考える.
ただし初期条件
を実数の定数とし,一つの漸化式を満たす数列の集合を考える.
ただし初期条件 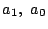 の値は実数とする.
の値は実数とする.
このとき 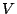 の要素
の要素 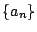 に対して平面ベクトル
に対して平面ベクトル
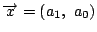 を
対応させることで
を
対応させることで 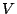 は平面ベクトルの全体と一致する.
は平面ベクトルの全体と一致する.
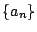 が
が
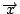 に対応し
に対応し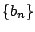 が
が
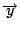 に対応していれば
に対応していれば
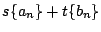 は
は
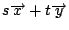 に対応する.
に対応する.
したがってこの対応で演算もそのまま対応する.
ゆえに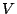 と平面ベクトルは同じものと見なすことができる.
平面ベクトルの集合を,実二次元ベクトル空間
と平面ベクトルは同じものと見なすことができる.
平面ベクトルの集合を,実二次元ベクトル空間 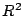 と書きあらわすと,
と書きあらわすと, 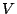 は,
ベクトル空間として
は,
ベクトル空間として 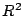 と同型である.
さて,任意の平面ベクトル
と同型である.
さて,任意の平面ベクトル
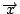 は,平行でない二つのベクトル
は,平行でない二つのベクトル
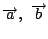 を用いて
を用いて
と表され,しかもこの表し方は一通りであった.
とくに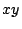 座標平面においては平行でない二つのベクトル
座標平面においては平行でない二つのベクトル
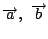 のなかで
のなかで
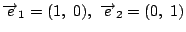 を「基底ベクトル」と呼ぶ.
を「基底ベクトル」と呼ぶ.
とすれば,8で定義された集合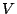 についても同じことが言える.
についても同じことが言える.
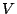 の任意の要素を二つの 数列
の任意の要素を二つの 数列
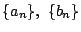 で
で
と表すためには,対応する 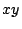 平面のベクトルが平行でなければよい.
そのような数列の組をいくつか求めよう.
平面のベクトルが平行でなければよい.
そのような数列の組をいくつか求めよう.
-
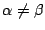 のとき.
のとき.
二つの 数列
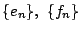 を
を
で定める.このとき 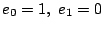 ,
,
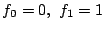 となるので,
一方が他方の定数倍ということはない.
となるので,
一方が他方の定数倍ということはない.
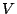 のすべての数列は,
数列
のすべての数列は,
数列
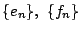 を用いて表される.
を用いて表される.
-
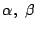 が実数で
が実数で
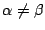 のときはさらに次のようにもできる.
のときはさらに次のようにもできる.
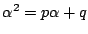 より
より
なので, 数列
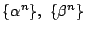 も漸化式を満たす.
も漸化式を満たす.
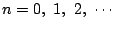 に対して数列
に対して数列
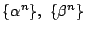 がともに
がともに 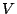 の要素になり,対応する
の要素になり,対応する 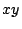 平面のベクトル
平面のベクトル
が平行でないので数列
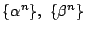 で
で
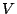 を表すこともできる.
を表すこともできる.
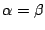 のとき.
つまり
のとき.
つまり
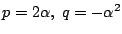 のとき.
のとき.
二つの 数列
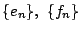 を
を
で定める.このときやはり 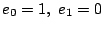 ,
,
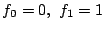 となり
となり
また, 数列
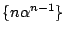 を考えると
を考えると
なのでこの数列も漸化式1を満たす.
数列
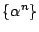 と数列
と数列
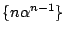 に対応する
に対応する
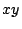 平面のベクトルは
平面のベクトルは
なので平行でない.ゆえにこの二つで 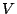 を表すことができる.
を表すことができる.
南海 最初の質問に関していえば,
(1) 拓生君の方法で求まる数列が最初の漸化式を満たすことと,
(2) 初期条件が同じものは一つしかないこと
をいえば,最初の定期テストの解答で解になっている.
またすでに気づいているとは思うが,
連立漸化式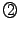 を解くことは,
を解くことは, から定まる行列
から定まる行列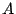 の
累乗
の
累乗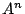 を求めることと同値である.
関係式
を求めることと同値である.
関係式 を,
あたかも三項間漸化式を等比数列を作って解くのと同じように変形していけば,
を,
あたかも三項間漸化式を等比数列を作って解くのと同じように変形していけば,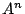 を直接求めることもできる.
その結果は
を直接求めることもできる.
その結果は
となる.



次: 固有値の方法
上: 三項間漸化式と行列の累乗
前: 三項間漸化式と連立漸化式
Aozora Gakuen
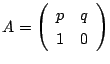 とする.
とする.
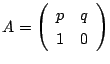 とする.
とする.
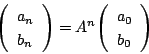
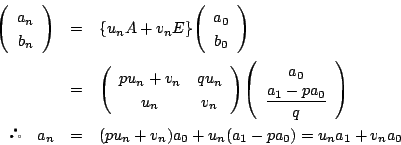
![]() の2解を
の2解を
![]() とする.つまり
とする.つまり
![]() のとき.
のとき.
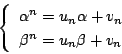
![]() のとき.
のとき.
![]() に対して,二次方程式
に対して,二次方程式
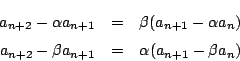
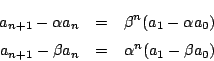
![]() の一般項を少し違う立場で考えよう.
2数
の一般項を少し違う立場で考えよう.
2数 ![]() と
二つの数列
と
二つの数列
![]() に対して数列
に対して数列 ![]() を
を
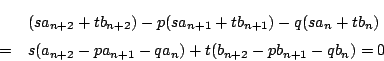
![]() と平面ベクトルは同じものと見なすことができる.
平面ベクトルの集合を,実二次元ベクトル空間
と平面ベクトルは同じものと見なすことができる.
平面ベクトルの集合を,実二次元ベクトル空間 ![]() と書きあらわすと,
と書きあらわすと, ![]() は,
ベクトル空間として
は,
ベクトル空間として ![]() と同型である.
さて,任意の平面ベクトル
と同型である.
さて,任意の平面ベクトル
![]() は,平行でない二つのベクトル
は,平行でない二つのベクトル
![]() を用いて
を用いて
![]() 座標平面においては平行でない二つのベクトル
座標平面においては平行でない二つのベクトル
![]() のなかで
のなかで
![]() を「基底ベクトル」と呼ぶ.
を「基底ベクトル」と呼ぶ.
![]() についても同じことが言える.
についても同じことが言える.
![]() の任意の要素を二つの 数列
の任意の要素を二つの 数列
![]() で
で
![]() を
を
![]() を
を
![]() と数列
と数列
![]() に対応する
に対応する
![]() 平面のベクトルは
平面のベクトルは
![]() を解くことは,
を解くことは,![]() から定まる行列
から定まる行列![]() の
累乗
の
累乗![]() を求めることと同値である.
関係式
を求めることと同値である.
関係式![]() を,
あたかも三項間漸化式を等比数列を作って解くのと同じように変形していけば,
を,
あたかも三項間漸化式を等比数列を作って解くのと同じように変形していけば,![]() を直接求めることもできる.
その結果は
を直接求めることもできる.
その結果は