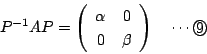
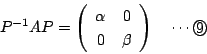
南海 いわゆる固有値の方法というものだ. 固有値を本当に理解しようとすれば,一次変換とベクトル空間についての理解がいる.『線形代数の考え方』を見てほしい.
ここでは二次行列の変形という範囲に絞って固有値の方法を話そう.
行列![]() に対して
に対して![]() の形に変形できるということはどういうことか.
行列
の形に変形できるということはどういうことか.
行列![]() を
を
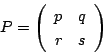
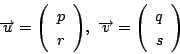
拓生
![]() は
は
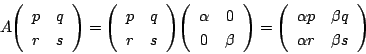
南海 そういうことだ.行列
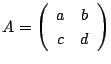 とおく.
とおく.
![]() は
は
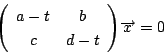
拓生 左辺の行列の![]() が0,つまり
が0,つまり
南海
これが相異なる二つの解
![]() をもつときは,
それぞれの
をもつときは,
それぞれの![]() の値に対して
の値に対して![]() を満たすようなベクトル
を満たすようなベクトル
![]() をとる.
をとる.
![]() は,
0でない実数倍だけとり方はあるが,いずれをとってもよい.
は,
0でない実数倍だけとり方はあるが,いずれをとってもよい.
この2つのベクトルを,
それぞれ![]() と
と![]() に対応する固有ベクトルという.
実数倍しても同じことなので,
行列
に対応する固有ベクトルという.
実数倍しても同じことなので,
行列![]() に固有な方向であると考えてもよい.
これで
に固有な方向であると考えてもよい.
これで![]() が求まり,連立漸化式などが解ける.
が求まり,連立漸化式などが解ける.
試しに次の連立漸化式を解いてほしい.
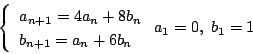
拓生
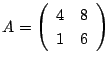 とおきます.まず
とおきます.まず![]() を対角化し連立漸化式を変形する.
を対角化し連立漸化式を変形する.
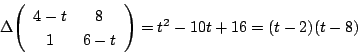
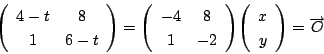
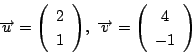
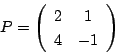
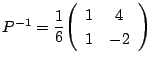 なので,
なので,
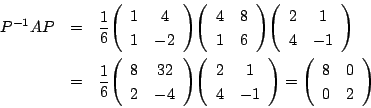
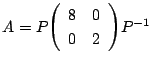 なので,連立漸化式
なので,連立漸化式
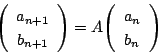
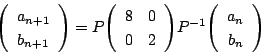
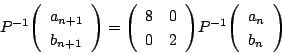
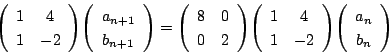
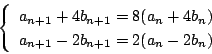
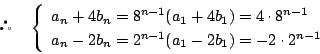
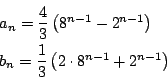
南海
もちろん![]() となるときも考えなければならならない.
また要するに固有値とは何か,についてもこのままではわからない.
それらについてはまた後日話すことにしよう.
となるときも考えなければならならない.
また要するに固有値とは何か,についてもこのままではわからない.
それらについてはまた後日話すことにしよう.