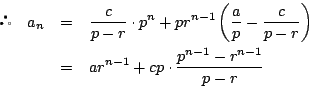もちろんその他にも
今考えるのは,漸化式が定数![]() と
と![]() の関数
の関数![]() を用いて
を用いて
この型の漸化式ですぐに解けるのはどのようなときか.
早苗
![]() で
で
![]() なら等差数列です.
なら等差数列です.
![]() なら数列
なら数列![]() は等比数列です.
は等比数列です.
これらは一般項が求まります.
![]() とすると,
とすると,
![]() で
で![]() のときは
のときは![]() です.
です.
![]() のときは
のときは![]() です.
です.
南海 その証明は?
早苗 えっ.そうかこれも数学的帰納法で示せばよい.
南海 そう.これはすぐにできる.
もうひとつ![]() のとき.これも教科書にのっている.
のとき.これも教科書にのっている.
早苗
はい.階差数列が
![]() となるので,
となるので,![]() のとき
のとき
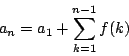
南海
以上の3つは![]() 型のうち簡単に解ける漸化式だ.
型のうち簡単に解ける漸化式だ.
その他の漸化式も,いろいろ変形を工夫して, このいずれかの解ける場合に持ちこむのだ.
そこで,
![]() 型の漸化式の解法をまとめよう.
型の漸化式の解法をまとめよう.
解き方は,大きく分けて3通りある.
それぞれについてまず一般的方法を述べて,
教科書にものっている
漸化式
![]() を
を![]() として解きながら説明しよう.
として解きながら説明しよう.
つまり
これを,
![]() をから辺々引くと
をから辺々引くと
これから数列![]() は公比
は公比![]() の等比数列なので,
の等比数列なので,
早苗 一つ見つけるといっても簡単ではありません.
南海
いや実は
![]() の場合,教科書はこの方法で解いている.
の場合,教科書はこの方法で解いている.
早苗
これは教科書では,
南海 これがまさに,解法1なのだ.
早苗
![]() は?….
そうかわかりました.
は?….
そうかわかりました.![]() で定数の数列です.
で定数の数列です.
南海 そうなのだ.
早苗
このとき![]() は
は
南海
この解法1は![]() が
が![]() の多項式のとき特に有効だ.
の多項式のとき特に有効だ.
![]() の次数を
の次数を![]() とする.
とする.![]() 次式
次式![]() を
を
早苗
![]() が
が![]() の多項式のときは,
一つの解自身が
の多項式のときは,
一つの解自身が![]() の多項式で得られるのですね.
の多項式で得られるのですね.
南海 f(n) が cpn の指数関数型でもこの方法が使える. それはあとの例でやろう.
早苗 これも難しく見えます.
この方法で
![]() を解くのはどうなるのですか.
この場合は
を解くのはどうなるのですか.
この場合は![]() なので
なので
これは要するに
![]() と
と
![]() から
から
![]() なので,
なので,
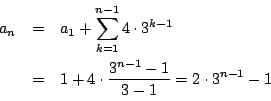
南海
階差をとる方法は![]() が
が![]() の
の![]() 次多項式のときにも有効だ.
次多項式のときにも有効だ.
早苗 でもそこから,階差数列を順に解いていくのは大変です.
南海
そうだ.![]() の1次式や2次式なら可能だが,それ以上になると不便だ.
の1次式や2次式なら可能だが,それ以上になると不便だ.
![]() の場合は,例題でやってみよう.
の場合は,例題でやってみよう.
もう一つ
![]() が
が![]() の定数係数の
1次式であることを生かす解法がある.
の定数係数の
1次式であることを生かす解法がある.
![]() の両辺を
の両辺を ![]() で割る.
で割る.
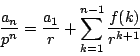
早苗
![]() などでは,
などでは,
![]() で割らずに,
で割らずに,![]() で割るのも習いました.
で割るのも習いました.
南海
0でない定数![]() で割って,
で割って,
早苗
![]() のような指数型のときは使えます.
のような指数型のときは使えます.
早苗
解法1
![]() でできないか考えてみます.
でできないか考えてみます.
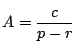 である.
つまり
である.
つまり
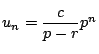 は一つの解である.
は一つの解である.
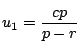 より,
より,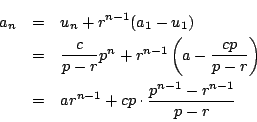
解法2
![]() で解法2を用いる.
で解法2を用いる.
![]() の両辺に
の両辺に![]() をかけ,
をかけ,![]() のときの漸化式から引く.
のときの漸化式から引く.
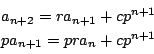
3項間漸化式から得られる2項間漸化式の一方がはじめの漸化式で,もう一つが新しく得られたものです.
解法3-1
漸化式の両辺を![]() で割る.
で割る.
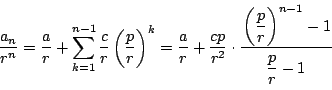
解法3-2
漸化式の両辺を![]() で割る.
で割る.
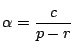 である.これから
である.これから