
 上: 問題を解く
前: 解ける根拠
上: 問題を解く
前: 解ける根拠
以上のことから解答が解答であるための必要にして十分な条件とは何かが明らかになってくる.問題は,共通な事実や全体で成立している条件で構成される前提のもとで何かを決定せよという形である.解答とは
前提の下で,求められた内容を決定し,その根拠を示す.
ことである.
前提,仮定,結論を自分自身に明確にし,求められていることを明確にすることが出発だ.
問題全体についても個々の論述についてもいえることだ.多くの問題はここをはっきりさせればそれで解法の見通しが立つ.そして結論を根拠とともに示す.これが解答だ.
根拠を示すのは論証のそれぞれの段階においても必要であり,解答全体として仮定条件から結論条件を導くことができているか,この両面で確認しなければならない.例えば確率の問題で「3個のサイコロを振る.和が3の倍数になる確率を求めよ」を解こうとする.このとき
サイコロの目の出方は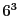 通りあり,そのうち和が3の倍数になるのは….
通りあり,そのうち和が3の倍数になるのは….
と論述を進める人が多い.しかし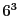 通りあるということも一つの結論である.この根拠は何か.やはり次のように進めるべきだ.
通りあるということも一つの結論である.この根拠は何か.やはり次のように進めるべきだ.
三つのサイコロを区別する.それぞれのサイコロの目の出方は6通りあり,各サイコロの目の出方は独立なので,サイコロの目の出方は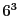 通りある.そのうち和が3の倍数になるのは….
通りある.そのうち和が3の倍数になるのは….
あるいは小問に分かれている確率などの問題で(1)ですべての場合の総数を問われて,何も理由を書かずに「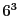 通り」とだけ書いて済ます人もたいへん多い.小問のはじめの方の問いこそていねいに根拠を書くべきなのだ.そうすると問題の全体がつかめる.サイコロを区別して数えるということをおさえることが,その後の計算を確実にするために必要なのだ.
通り」とだけ書いて済ます人もたいへん多い.小問のはじめの方の問いこそていねいに根拠を書くべきなのだ.そうすると問題の全体がつかめる.サイコロを区別して数えるということをおさえることが,その後の計算を確実にするために必要なのだ.
例えば次のような過去問題がある.出典を知らないのであるがいい問題だ.
例題 2.6
[出典不明]
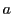 は実数の定数とする.
は実数の定数とする.
で定まる数列
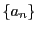
について,次の問いに答えよ.
- 一般項
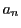 を
を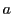 と
と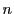 の式で表せ.
の式で表せ.
- 任意の自然数
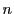 に対し,
に対し,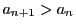 が成り立つときの
が成り立つときの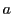 の値を求めよ.
の値を求めよ.
これは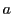 の条件を求めよということなのだが,見落としやすいところがある.条件といえばそれは必要十分条件なのだ.
の条件を求めよということなのだが,見落としやすいところがある.条件といえばそれは必要十分条件なのだ.
解答
- 漸化式を
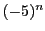 で割って
で割って
これから
なので,
これは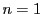 でも成立する.
でも成立する.
-
がすべての自然数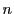 で成立すればよい.
で成立すればよい.
これは
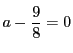 なら成立する.
よって
なら成立する.
よって
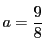 は十分条件である.
は十分条件である.
必要条件でもあることを示す.
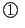 を
を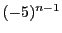 で割って整理する.
で割って整理する.
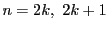 に応じて
に応じて
これがすべての自然数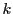 で成立する.これから
で成立する.これから
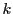 を大きくすると,
を大きくすると,
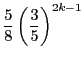 はいくらでも小さくなるので,
はいくらでも小さくなるので,
が必要である.
ゆえに
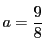 は必要十分条件である.
□
は必要十分条件である.
□
このような論理に関する感覚的な鋭さを養いたい.以上で問題とは何かを考えた.
それでは数学の問題を解く一般的な方法はあるのか.それはない.それがあれば何も考えることはない.数学は客観的に存在している.記述法や形式はいろいろあっても,それを可能にしている数学的存在は確かにある.人間は自然を探求するように数学を探究してきた.
入試問題など高校数学の問題は,作り出された問題であり,結果はあらかじめ出題者にはわかっている.したがって高校数学の問題は必ず解ける.高校数学の問題は,一つは理解を助けるためにあり,一つは問題を分析して系統立てて解く力を訓練するためにある.そこで求められる力は,この先いろんな分野で能動的に生きていくために必要なものに他ならない.ならばいくつかの基本的な方法を定式化し,それを身につけていくことは,単に数学ができるようになる以上の意味をもつことになる.そのためにいくつかの方法をできるだけ系統的に考えていこう.
数学の問題を解こうとするとき,どこから手をつけていいか見当もつかなかったり,あるいは逆にやみくもに試行錯誤したり,いずれにしても系統立てて問題に取り組むということがなかなかできない.数学の問題というのはそれ自身構造をもっている.まず問題の構造を見抜くことである.それによって問題を解く道筋も定まってくる.もちろん一般に一つということはないのだが,問題の構造が正確に見えれば,半ば解けたといってよい.構造を見抜き解法の道筋を発見する補助手段として,いくつかの方法がある.
新しい問題に出会ったとき,ここで勉強した方法を意識的に適用してみてほしい.それができればずいぶん力が伸びたことを実感できるだろう.その方法を次のように分類して順次その内容を考えるとともに,近年の入試問題を演習問題として考え方とともに紹介する.
- 前提,成立が仮定される条件,結論として成立を示すべき条件を整理する.
これは当然の作業である.
そのうえで,それらの諸条件は一体どのようにからみあっているのか.
それが問題の構造であるが,それを見ぬかなければならない.
そのためにいくつか試してみるべき方法,視点というものがある.
それが問題解決の糸口である.典型的な方法をまとめる.
- ある程度の見通しができたら,論証を進めなければならない.
論証とは,仮定条件から結論条件へ同値変形をくりかえして道筋をつけることである.
必要性だけを問うているときもあるが基本は同値変形である.
それ自体が道筋に沿った問題の探求である.
そのための補助となるいくつかの論証推進のための方法を整理する.
- 数学の問題というのはどんなに小さなものであれ,
それ自身一つの数学的現象である.
そのような現象を引き起こす内部構造をもつ.
どのような構造がそこで働いているのか.
この観点から問題を見る.この力をつけるために,
高校数学で習う典型的な構造について,
内部構造の分析を試みる.
それをいかした論証の方法を学ぶ.
これらについて,解説と例題,演習問題とその解答で進めたい.
この『高校数学の方法』では考え方を学ぶので,整式関数以外の微分積分は扱わない.
また,教科書と学校で入手した問題集を一通りやった段階を仮定している.
それぞれの解答は,その項目の方法の実践であるが,
またまったく別の方法があるときもある.
他の方法があるときはできるかぎり別解も紹介する.
異なる問題を二題解くよりも一題を二通りの方法で解く方が力がつく.
日頃からつねに別解を考えるようにしてほしい.
Aozora
2018-02-25
通りあり,そのうち和が3の倍数になるのは….
通りある.そのうち和が3の倍数になるのは….
![]() 通り」とだけ書いて済ます人もたいへん多い.小問のはじめの方の問いこそていねいに根拠を書くべきなのだ.そうすると問題の全体がつかめる.サイコロを区別して数えるということをおさえることが,その後の計算を確実にするために必要なのだ.
通り」とだけ書いて済ます人もたいへん多い.小問のはじめの方の問いこそていねいに根拠を書くべきなのだ.そうすると問題の全体がつかめる.サイコロを区別して数えるということをおさえることが,その後の計算を確実にするために必要なのだ.
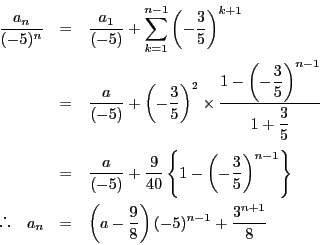
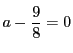 なら成立する.
よって
なら成立する.
よって
![]() は十分条件である.
は十分条件である.
![]() を
を![]() で割って整理する.
で割って整理する.
![]() に応じて
に応じて
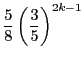 はいくらでも小さくなるので,
はいくらでも小さくなるので,