![]() と
と![]() を整数,
を整数,![]() を素数とする.
を素数とする.![]() が
が![]() で割り切れれば,
で割り切れれば,![]() または
または![]() が
が![]() で割り切れることを証明せよ.
で割り切れることを証明せよ.
数学の力をつけるためには,普段用いている公式や,日頃証明することなく用いている事実を,時には立ち止まって考えなおしてみることである.それを自分でやっていく人は,どんどん力をのばしてゆくことができる.
例えば次の問題はどのように解くだろうか. これは数論の基本事項である.
![]() と
と![]() を整数,
を整数,![]() を素数とする.
を素数とする.![]() が
が![]() で割り切れれば,
で割り切れれば,![]() または
または![]() が
が![]() で割り切れることを証明せよ.
で割り切れることを証明せよ.
これなど日頃は当然のように用いている.改めて示そうとすると,何を根拠に解けばよいのかわからない.![]() が素数であるということは,
が素数であるということは,![]() の約数が1と
の約数が1と![]() 以外にないということであり,これは整数
以外にないということであり,これは整数![]() 自身の内在的な性質だ.そのような性質をもつ
自身の内在的な性質だ.そのような性質をもつ![]() が二つの整数の積
が二つの整数の積![]() の約数になれば,
の約数になれば,![]() か
か![]() 少なくとも一方の約数になっている,これは
少なくとも一方の約数になっている,これは![]() と他の整数との関係だ.
と他の整数との関係だ.
ここに難しさがある.
解答
![]() が
が![]() で割り切れるので,
で割り切れるので,![]() の素因数分解には
の素因数分解には![]() が現れる.
が現れる.
![]() も
も![]() が
が![]() で割り切れないとすると,
で割り切れないとすると,
![]() の素因数分解にも
の素因数分解にも![]() の素因数分解にも
の素因数分解にも![]() が現れず,
その結果,積
が現れず,
その結果,積![]() の素因数分解に
の素因数分解に![]() が現れない.
が現れない.
これは素因数分解の一意性と矛盾する.
よって![]() か
か![]() の少なくとも一つは
の少なくとも一つは![]() の倍数である.
□
の倍数である.
□
ここでは素因数分解の一意性を根拠にした.つまり,どのような順に因数を見つけていったとしても,素数の積に分解できた段階で,順番を除いて因数分解は一通りに定まる,そして,そのことから導かれる積の素因数分解は素因数分解の積と順序を除いて一致するということである.大学入試問題を解くときには素因数分解の一意性は証明せずに用いてもよい.
しかし,ではこの素因数分解の一意性はどのように示されるのか.素因数の個数に関する数学的帰納法がひとつの方法である.このところは『整数の基本』,『数論初歩』を見てほしい.
例えば等式の中に未知な文字が3個あるとき,独立な等式も3個あれば基本的に問題は解ける.問題を解くときに,未知数の個数と条件の個数を確認しているか.与えられた条件から未知数を確定するのに必要な未知数の個数だけの等式をどのように導くのか,問題を解くときにはこのように考えを進めたい.問題をそのまま解きはじめるのではなく,解が決定できる根拠を考えつつ,少し高い視点を持ちながら解く.
このように問題を読んだ段階で「なぜこの問題は解けるのか」を考えることをすすめたい.入試問題なので解けるに決まっている.解けない問題は問題としてまちがっているということになる.しかし解ける根拠を考えることで方法が発見されるのだ.
実際に何か新しいことを研究するときは解けるとはかぎらないし,人が生きていくのに,解けないかも知れない問題に立ち向かわなければならないことはしょっちゅうある.解けないどころかあまりに理不尽なことに直面することも多々ある.それが現実だ.
が,とにかく入試問題は解ける.解けるはずだからといってすぐ解こうとしても解けない.そこで「解ける根拠はどこにあるのか」を考える.そのことによって解き方がわかってしまうということがよくあるのだ.「解ける根拠」は必ず問題の中にある.
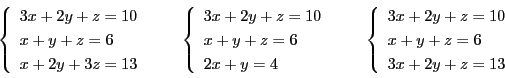
「満たす実数![]() 」の個数である.つまり,集合
」の個数である.つまり,集合![]() を
を
本問の方程式は4次であり,根の個数は複素数の範囲で重複したものを重ねて数えると必ず4個である.本問は,そのうち相異なる実数根はいくつあるかということなので有限個に確定することはまちがいない.(1)は成り立つ.本問のように一定の条件(今の場合は方程式)を満たすものをすべて求めよ,またその個数を求めよといった型の問題では,(1)は「確かに有限個に確定する」ということになることが多い.
4次方程式の根が重なるのは,因数に分解された各2次方程式の少なくとも一方が重根をもつときと,二つの2次方程式に共通根がある場合である.方程式の共通根を求める方法は,共通根があるとしてそれを必要条件で絞り,確認する.2次方程式なのでかならずできる.これが(2)である.
![]() 次方程式
次方程式
それに対して解とは「方程式を満たすもの」で,実質は集合
40年前は中学でも「2次方程式の根」と正しくいっていた.正しい使い方に戻ることを願っている.本問は実数解の個数を数えよということなのだ.さて解答である.
解答
2つの2次方程式
2つの方程式に共通解があるとしてそれを![]() とおく.
とおく.
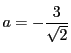 .
.
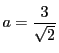 .
これらのときそれぞれの他の1解は異なる.
以上から方程式を満たす実数
.
これらのときそれぞれの他の1解は異なる.
以上から方程式を満たす実数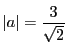 のとき,3個.
のとき,3個.
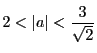 または
または
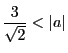 のとき,4個.
のとき,4個.
なお本問はグラフを用いる別の解法もある.同様の問題が理系乙でも出題されたので,2章3節「関係の図示」の問題に入れておく.問題![[*]](images/crossref.gif) である.
である.
次に確率の問題を見てみよう.
白黒2種類のカードがたくさんある.
そのうち![]() 枚のカードを手もとにもっているとき,
次の操作(A)を考える.
枚のカードを手もとにもっているとき,
次の操作(A)を考える.
この問題が解ける根拠は問題が与えた操作(A)の中の「等確率」というところである.つまり1枚1枚のカードが選ばれる確率はその場に何枚のカードがあるかだけで決まる.何回この操作を繰り返した後でもこれは変わらない.![]() 回目のいくつかの状態から
回目のいくつかの状態から![]() 回目のいくつかの状態への推移の確率が,
回目のいくつかの状態への推移の確率が,![]() によらず一定であるといういわゆるマルコフ過程となり,
によらず一定であるといういわゆるマルコフ過程となり,![]() による確率のあいだに漸化式を立てることができる.漸化式は最初のいくつかの値(初期値)によって数列を決定する.漸化式が出来るということによって(1)がわかる.その漸化式が解けることによって(2)が確認される.
による確率のあいだに漸化式を立てることができる.漸化式は最初のいくつかの値(初期値)によって数列を決定する.漸化式が出来るということによって(1)がわかる.その漸化式が解けることによって(2)が確認される.
解答
以下白![]() 枚,黒
枚,黒![]() 枚である事象を
枚である事象を![]() とかく.
とかく.
![]() 回繰り返した後に初めて,4枚とも同じ色のカードになるのは
回繰り返した後に初めて,4枚とも同じ色のカードになるのは
![]() 回繰り返した後
回繰り返した後![]() か
か![]() であって,
であって,
![]() 回目に1枚ある方の色を変える場合である.
回目に1枚ある方の色を変える場合である.
![]() とおき,
とおき,![]() 回繰り返した後,
回繰り返した後,
![]() か
か![]() である確率を
である確率を![]() とおく.
とおく.
![]() 回繰り返した後も
回繰り返した後も![]() か
か![]() のいずれかであるので,
のいずれかであるので,
![]() ,
,![]() ,
,![]() の間の変化とその確率は次のようになる.
の間の変化とその確率は次のようになる.
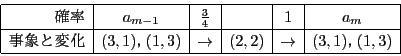
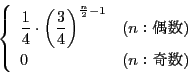
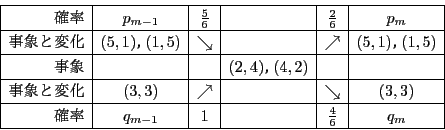
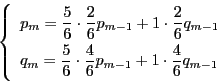
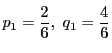 なので,
この結果
なので,
この結果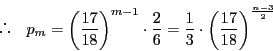
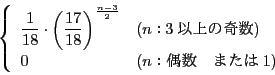
少し脱線.数学の世界では「リーマン予想」とか「ゴールドバッハ予想」とか「予想」といわれるものがある.それは証明できるだろう,こういうことが成り立つだろうと「予想」されるのであるが,その予想の真偽を決定することは,その時点では出来なかったからこそ「予想」になる.
一方「フェルマーの最終定理」というのがある.17世紀の人フェルマーは,古代ギリシャのディオファントスの書物の余白に
2よりも大きなべき指数と書き込んだ.ここに言う「べき指数について,
をみたす三つの整数
を見出すことは不可能である.私はこれについてのまったくすばらしい証明を得たが,ここの余白は狭すぎて書き記すことができない.
350年もの間解決出来なかった.1994年に至ってプリンストン大学のアンドリュー・ワイルズがついに完全な証明に成功した.その証明は日本の数学者の谷村豊と志村五郎が打ち出した原理にもとずいていた.このように歴史に残る大問題は,証明可能性自体が問題であった.
さてわれわれが考える入試問題などでは,証明可能であることはまちがいない.問われていることは確実な論証構成力である.とくに京大のように小問に分けず,大問一つで出題するところは,このような問題分析能力を求めているということを心得ておきたい.