![]() が実数のとき次の二つの2次方程式
が実数のとき次の二つの2次方程式
が共通解をもつための条件とそのときの共通解を求めよ.
![]() が実数のとき次の二つの2次方程式
が実数のとき次の二つの2次方程式
考え方 共通解があるとして,それを文字に置く. ここから得られる結果は必要条件だ. 必要条件として何を引き出すかは, いろいろ工夫のしどころである. そのうえで,得られた結果の十分性を確認していく.
解答1
共通解が存在するとし,それを![]() とおく.
とおく.
![]() のとき.
のとき.![]() も成り立ち
も成り立ち![]() を消去すると
を消去すると
![]() .
.![]() が実数なので
が実数なので![]() .
.![]() .
このとき両式は一致し,
共通解は
.
このとき両式は一致し,
共通解は
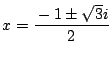 .
.
![]() のとき.
のとき.
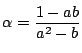 が必要である.
これから
が必要である.
これから
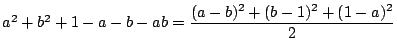 より,
係数は実数なのでこれが0になるのは
より,
係数は実数なのでこれが0になるのは
求める条件と共通解は

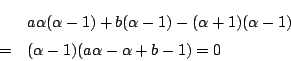
![]() のとき.
のとき.
![]() なら
なら![]() で,
このとき両式は一致し,共通解は
で,
このとき両式は一致し,共通解は
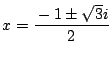 .
.
![]() なら
なら
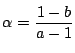 が必要.
が必要.
よって同様の解を得る. □
![]() のとき.条件は
のとき.条件は![]() .
.
![]() のとき.
のとき.
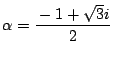 または
または
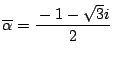 .
係数が実数なので一方が共通解なら他方も共通解である.
.
係数が実数なので一方が共通解なら他方も共通解である.
第1の方程式で解と係数の関係から
よって同様の解を得る. □
このように「何をどう置くか」と考え式を立てることが, 問題解決の第一歩である. 式を立てようとすることで問題を解きほぐす糸口が見つかることが多い. したがって,今後いろんな所で目的意識をもってこれを試してほしい.