

 次: 等しいものを文字に置く
上: 糸口をつかむ
前: 糸口をつかむ
次: 等しいものを文字に置く
上: 糸口をつかむ
前: 糸口をつかむ
記号,これは人間が見つけ出したすばらしい道具である.
企業や学校などいろんな組織の標章にはじまりパソコンや携帯電話のアイコンまで,
現代社会は記号としての文字,標章,符号などにあふれている.
制服なんかも記号の一種である.
記号は何か「同じもの」であることを示すのに用いられる.
数学でも同じだ.
概念,数式,命題などを書き表わすために符号を用いる.
三つの数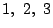 の集まりを集合という考え方で把握し,
さらにそれを
の集まりを集合という考え方で把握し,
さらにそれを
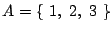 のように一つの記号
のように一つの記号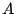 で表す.
ここには,抽象的な人間の精神活動の歴史と発展がこめられている.
この場合三数を括弧
で表す.
ここには,抽象的な人間の精神活動の歴史と発展がこめられている.
この場合三数を括弧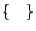 でくくるという行為をしている.
何かの集まりを一つのこととしてつかみ,
一段高いところからまとめる作用を括る(kukuru)働きという.
これは人間の心(kokoro)の最も基本的な働きである.
括弧でくくる作用は,
くくられた内容がひとまとまりのものであることを認識するという
抽象作用が第一で,
ひとまとまりであるから,これに一つの符丁をつけるという作用が第二である.
この符丁が記号である.
記号は心の働きの必然の結果である.
でくくるという行為をしている.
何かの集まりを一つのこととしてつかみ,
一段高いところからまとめる作用を括る(kukuru)働きという.
これは人間の心(kokoro)の最も基本的な働きである.
括弧でくくる作用は,
くくられた内容がひとまとまりのものであることを認識するという
抽象作用が第一で,
ひとまとまりであるから,これに一つの符丁をつけるという作用が第二である.
この符丁が記号である.
記号は心の働きの必然の結果である.
文字記号は定数,変数,未知数などいろいろの働きをしているが,
文字記号で表すということ自体が一つの抽象である.
さらに,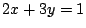 ,
,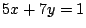 ,
,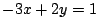 などの形から,
などの形から,
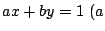 と
と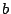 は互いに素な整数)と表すのは,
そこに共通な一般的な形を見いだしている.
これがこころの働きであり,数学の基礎である.
は互いに素な整数)と表すのは,
そこに共通な一般的な形を見いだしている.
これがこころの働きであり,数学の基礎である.
記号は普通は文字で表す.
日本語では日本文字と区別して西洋文字を使うことが多い.
見分けがつきやすく便利である.
「日本語のなかで,西洋文字で表した記号を使いこなす」ことが,
ある意味ではこれが高校数学の目的である.
入学試験の数学問題は,もちろんいろんな分野から出題されるが,
基調にあるのは,
「問題文に書かれた数学的事実を読み取り,文字記号を用いて式に表し,
その式を操作して必要な結論を引き出せる」
かどうかを判定するということである.
題意をつかみ,成立している条件を式に表す.
同時に,証明すべき結論も式に表す.
そして条件式から結論を決定する.
これが問題を解く基本である.
だから,問題を解こうとするとき,
まず最初に考えなければならないのは,
問題文を数式等の数学用語に翻訳するためにどのような設定をするか,
つまり,何をどにように置くか,である.
ここからはじめて,文字で考えることで,
問題解決の糸口を見いだし,論証を進めることを学ぼう.
問題文をよく読んだら,
一息おいてこの問題を解くのに何をどう置けばよいのか考える.
一つの置き方が見つかっても,他によりいい方法がないかも考える.
どう置くのかと考えることで,何がいちばん基本的な変数かとか,
何が決まれば全体が決まるかとか,
いろんな変数の相互関係を調べることになる.
「平面上に2点
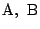 があり,
線分
があり,
線分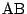 上に点
上に点 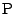 がある.」これは日本語である.
これを「数学の言葉」に翻訳しなければならない.
どんな翻訳があるか.
がある.」これは日本語である.
これを「数学の言葉」に翻訳しなければならない.
どんな翻訳があるか.
- 点
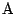 を原点,点
を原点,点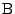 を
を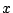 軸上にとり,
線分
軸上にとり,
線分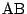 を座標平面に置く.
を座標平面に置く.
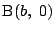 とする.
線分
とする.
線分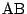 上の点
上の点 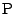 を
を
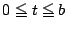 の範囲の実数
の範囲の実数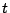 を用いて
を用いて
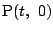 と置く.
と置く.
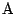 を始点とするベクトルで考える.
線分
を始点とするベクトルで考える.
線分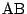 上の点
上の点 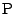 を
を
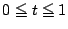 の実数
の実数 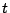 を用いて,
を用いて,
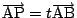 と置く.
と置く.
等いろいろある.
もちろん図形の論証でいくのなら,
平面上に線分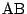 をおいて,
そのうえの点
をおいて,
そのうえの点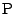 を指示するところからはじめることになる.
座標で考えるか,ベクトルで考えるか,図形の論証か,
この先の展開を考え適切な設定をすることが必要である.
このように「さあ,問題を解こう」とするとき,
まず最初に考えなければならないのは
何をどう置くかである.
を指示するところからはじめることになる.
座標で考えるか,ベクトルで考えるか,図形の論証か,
この先の展開を考え適切な設定をすることが必要である.
このように「さあ,問題を解こう」とするとき,
まず最初に考えなければならないのは
何をどう置くかである.
適当な文字の導入によって,
問題の条件や結論を数式の言葉に翻訳することを考える.
数学が苦手な人は,
この「置きかえによる問題文の式への翻訳」が苦手な場合がほとんどである.
問題に対して適切に文字を置き,
式に翻訳できれば三分の一は解けたようなものだ.
しっかり勉強して,次のような考え方を身につけよう.
- 複雑な式のなかから共通の形を見いだし,
それを別の文字で置き換える.
- いくつかの式のとる値が等しいとして与えられている条件は,
この等しい値を文字で表す.
- 変化する量があればその量を変数で表す.
未知量を求めるときは,方程式として解く.
- 条件が「何々が存在する」とあれば,
存在するものを文字に置き,存在する必要条件を求める.
- 図形を一般性を失わないで,
できるだけ単純な式になるように座標平面に置く.
- 考える対象が量の関係なら,変数を導入し,
他の量との関係を調べ,関数形に表す.
- 座標のなかで動きのあるものを,
適当な変数(媒介変数,パラメーター)で表す.
- 自然数
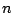 によって定まる場合の数や確率は
によって定まる場合の数や確率は
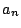 など数列におく.そのうえで漸化式を考える.
など数列におく.そのうえで漸化式を考える.
このなかで(2),(3),(4)は文字におく典型的な場合である.
以下でもう少し詳しく説明し,例題をあげる.
Aozora Gakuen
![]() の集まりを集合という考え方で把握し,
さらにそれを
の集まりを集合という考え方で把握し,
さらにそれを
![]() のように一つの記号
のように一つの記号![]() で表す.
ここには,抽象的な人間の精神活動の歴史と発展がこめられている.
この場合三数を括弧
で表す.
ここには,抽象的な人間の精神活動の歴史と発展がこめられている.
この場合三数を括弧![]() でくくるという行為をしている.
何かの集まりを一つのこととしてつかみ,
一段高いところからまとめる作用を括る(kukuru)働きという.
これは人間の心(kokoro)の最も基本的な働きである.
括弧でくくる作用は,
くくられた内容がひとまとまりのものであることを認識するという
抽象作用が第一で,
ひとまとまりであるから,これに一つの符丁をつけるという作用が第二である.
この符丁が記号である.
記号は心の働きの必然の結果である.
でくくるという行為をしている.
何かの集まりを一つのこととしてつかみ,
一段高いところからまとめる作用を括る(kukuru)働きという.
これは人間の心(kokoro)の最も基本的な働きである.
括弧でくくる作用は,
くくられた内容がひとまとまりのものであることを認識するという
抽象作用が第一で,
ひとまとまりであるから,これに一つの符丁をつけるという作用が第二である.
この符丁が記号である.
記号は心の働きの必然の結果である.
![]() ,
,![]() ,
,![]() などの形から,
などの形から,
![]() と
と![]() は互いに素な整数)と表すのは,
そこに共通な一般的な形を見いだしている.
これがこころの働きであり,数学の基礎である.
は互いに素な整数)と表すのは,
そこに共通な一般的な形を見いだしている.
これがこころの働きであり,数学の基礎である.
![]() があり,
線分
があり,
線分![]() 上に点
上に点 ![]() がある.」これは日本語である.
これを「数学の言葉」に翻訳しなければならない.
どんな翻訳があるか.
がある.」これは日本語である.
これを「数学の言葉」に翻訳しなければならない.
どんな翻訳があるか.