階差を取る作用は
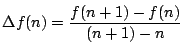 としてみればわかるように,
関数の導関数を考えることに対応している.実は「階差をとる」ことを「差分する」ともいうのだが,これは言うまでもなく「微分する」と対応する言葉の使い方だ.
ついでながら階差数列からもとの数列を見出す
としてみればわかるように,
関数の導関数を考えることに対応している.実は「階差をとる」ことを「差分する」ともいうのだが,これは言うまでもなく「微分する」と対応する言葉の使い方だ.
ついでながら階差数列からもとの数列を見出す
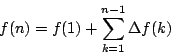
そこで次の問題を考えよう.
例題 2.13 [00京大文系]
実数
![]() が条件
が条件
考え方
最初に問題の条件を階差の関係
 その次にこの階差数列の不等式は何を意味しているかだ.
その次にこの階差数列の不等式は何を意味しているかだ.
階差が増加している.微分が増加している.二次導関数が正.下に凸なグラフ.と理系の人なら 連想が進むかも知れない. が,これは文系の問題だ.階差が増加しているようなグラフをかいてみよう. 階差が増加しているということは,数列が減少しているときは減少幅が小さくなり, 数列が増加しているときは増加幅が大きくなることだ.
これでわかる.実際下に凸な折れ線になる.形としては①のようにはじめ減少で
途中から増加に転じる場合,途中の1カ所で![]() となればそこで最小になり
最小値をとる
となればそこで最小になり
最小値をとる ![]() の個数は2個,
の個数は2個,
![]() なら1個.②や
③の形なら
なら1個.②や
③の形なら ![]() か
か ![]() の1個のみとなる.
の1個のみとなる.
解答
題意の条件は
![]() は単調減少で,
は単調減少で,
![]() は単調増加.
よって
は単調増加.
よって ![]() となり他に
となり他に ![]() となるものはない.この場合は1個.
となるものはない.この場合は1個.