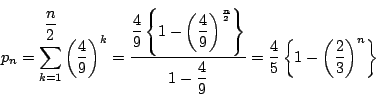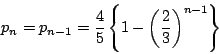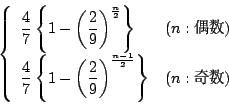「一つのサイコロを振り,出た目が4以下ならばAに1点を与え,5以上ならばBに1点を与える」 という試行を繰り返す.
- AとBの得点差が2になったところでやめて得点の多い方を勝ちとする.
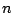 回以下の
試行でAが勝つ確率
回以下の
試行でAが勝つ確率 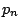 を求めよ.
を求めよ.
- Aの得点がBの得点より2多くなるか,またはBの得点がAの得点より1多くなったところで
やめて,得点の多い方を勝ちとする.
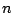 回以下の試行でAが勝つ確率
回以下の試行でAが勝つ確率 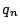 を求めよ.
を求めよ.
次の例題などは試行の過程を図にして考えないと困難だ.
「一つのサイコロを振り,出た目が4以下ならばAに1点を与え,5以上ならばBに1点を与える」 という試行を繰り返す.
解答
(1)
![]() 軸に回数
軸に回数 ![]() ,
,![]() 軸に得点差
軸に得点差 ![]() を取り,点
を取り,点![]() を平面にとる.
するとこの試行は,平面上の点の移動としてとらえることができる.
点
を平面にとる.
するとこの試行は,平面上の点の移動としてとらえることができる.
点![]() から点
から点![]() へ移動する確率は
へ移動する確率は ![]() ,
点
,
点![]() から点
から点![]() へ移動する確率は
へ移動する確率は ![]() になる.
になる.
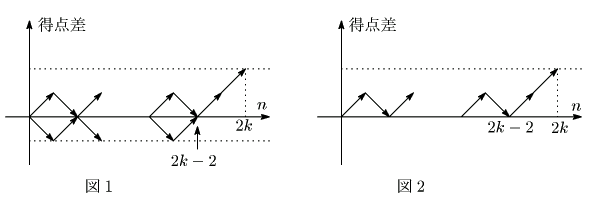
このようにすると,
得点差が ![]() の間をくり返し,最後にAが2連勝するしか
得点差が2になることはない.したがって,奇数回目の得点差は奇数なので,得点差が2になるのは,
偶数回目しかないことがわかる.
の間をくり返し,最後にAが2連勝するしか
得点差が2になることはない.したがって,奇数回目の得点差は奇数なので,得点差が2になるのは,
偶数回目しかないことがわかる. ![]() 回目にAが勝つ確率
回目にAが勝つ確率 ![]() は,
は,