次: 図形の論証方法 上: 構造の分析 前: 構造の分析

図形とは何か

図形は点の集合

平面図形，関数のグラフ，直線，放物線，円，軌跡，領域， と図形問題はつねに出てくる． これに対してそれぞそれ個別に対応しているのがほとんどの場合だ． しかしこれらには共通のことがある． 図形とは一定の条件を満たす点の集合だということだ． この観点をしっかりもっておくことが必要である．

$$図形＝\{点 \mathrm{P}\ \vert\ \mathrm{P}は一定の条件を満たす\}$$

例えば円は，

$$点\mathrm{O}からの距離が等しい， という条件を満たす点\mathrm{P}の集合．$$

として定義される． これを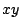$xy$座標の方程式で表せば，

$$方程式\ x^2+y^2=r^2\ を満たす点\ (x,\ y)\ の集合．$$

としても定義される．方程式もまた変数に関するひとつの条件である．

図形の性質とはその点の集合に何らかの規則性や構造を見出し， それを点の集合の性質としてつかんだものである．だから

$$図形の探求＝点の集合の構造の探求$$

ということである． ここでは， 条件を満たす点の集合としての図形のとらえ方と その構造を探求する方法を学ぼう．

• 図形の論証方法
• 値域・軌跡・通過範囲
• 問題と考え方