この観点から,値域・軌跡・通過範囲を統一的に把握しよう. これは,問題の構造をよく見て論理的に考える練習になる.
問題を解きながら,普通はどのようにいわれているのか,考えていこう. あえて問題にあわせた解答をしていく.
解答
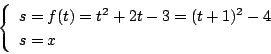
![]() となり,グラフの軸が
となり,グラフの軸が ![]() である. したがってここでは単調増加なので
である. したがってここでは単調増加なので
![]() の連立方程式と見て解く.
の連立方程式と見て解く.
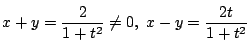 なので
なので
解2
![]() となる
となる ![]() が存在するのは
が存在するのは
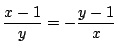 より
より
本問の図形が「 ![]() が実数を動くときの二直線の交点の軌跡」というものだ.
「軌跡」といっても「点の集合」であることに変わりない.
が実数を動くときの二直線の交点の軌跡」というものだ.
「軌跡」といっても「点の集合」であることに変わりない.
求める ![]() であることは,
であることは,
![]() となる
となる ![]() の範囲の
の範囲の ![]() が存在することと同値である.
が存在することと同値である.
ゆえに![]() の二次方程式
の二次方程式 ![]() が
が ![]() に解をもつような
に解をもつような
![]() に他ならない.
に他ならない. ![]() とおく.次のいずれかが成り立てばよい.
とおく.次のいずれかが成り立てばよい.
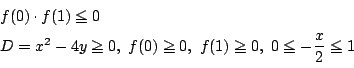
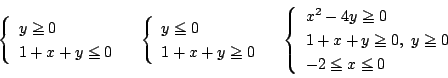
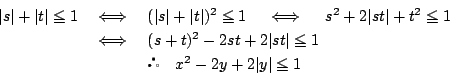
![]() は,
は, ![]() なら
なら ![]() ,
, ![]() なら
なら![]() を意味する.
を意味する.
これは「領域から領域への写像」だ.

通常「値域,軌跡,通過範囲」といわれるものもこのように言い方や見方をかえれば, 同じ型の問題であることは理解できただろうか.
![]() を数直線や座標平面,またはその部分集合とする.
を数直線や座標平面,またはその部分集合とする.
![]() の要素を動く変数
の要素を動く変数 ![]() と
と ![]() の要素を動く変数
の要素を動く変数 ![]() の間の関係式がある
(一つとはかぎらない)とする.この関係式を
の間の関係式がある
(一つとはかぎらない)とする.この関係式を ![]() と象徴的に書こう.象徴的というのは,式が一つとはかぎらないからである.
また,
と象徴的に書こう.象徴的というのは,式が一つとはかぎらないからである.
また, ![]() や
や ![]() と大文字を使ったのは,
と大文字を使ったのは,
![]() のような平面の点(二変数)のこともあるからだ.
一変数のときは小文字を使うのが普通だが統一的に大文字にした.
のような平面の点(二変数)のこともあるからだ.
一変数のときは小文字を使うのが普通だが統一的に大文字にした.
![]() は通常のいい方では媒介変数にあたる.
は通常のいい方では媒介変数にあたる.
この観点から例題の(1)(2)(3)を再度一般的な命名と問題の形にまとめる.
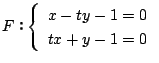 で定まる
で定まる
このように上の問題はどれも次の形をしている,
集合集合で書けばと集合
の要素の間に一定の関係があるときに,
の部分集合
の各要素とこの関係で対応する
の要素の集合
を求めよ.
受験参考書ではこのようにして媒介変数の存在条件として ![]() を求める方法を
「逆像法」とか「逆手法」とかいうことが多い.
何となく「裏ワザ」的な名前がついているため,
正面から勉強しないことが多いようだが,
この方法こそ問題の構造を論理的に解明する「正攻法」なのだ.
これがときに応じて値域であり,軌跡であり,通過領域,ということだ.
値域とか,軌跡とか,通過領域とか,
いろいろに訳すのは日本の高校数学ぐらいなもので,
かえってわかりにくくなっている.
大切なことは,
この
を求める方法を
「逆像法」とか「逆手法」とかいうことが多い.
何となく「裏ワザ」的な名前がついているため,
正面から勉強しないことが多いようだが,
この方法こそ問題の構造を論理的に解明する「正攻法」なのだ.
これがときに応じて値域であり,軌跡であり,通過領域,ということだ.
値域とか,軌跡とか,通過領域とか,
いろいろに訳すのは日本の高校数学ぐらいなもので,
かえってわかりにくくなっている.
大切なことは,
この![]() は媒介変数
は媒介変数![]() が存在するための条件として定まるということだ.
が存在するための条件として定まるということだ.
ただしあくまで「定まる」ということであって, 具体的に求まるかどうかは別の問題である. 例えば『数学対話』のなかの「包絡線」で取りあげた通過領域は, この方法では具体的には求まらなかった. そこでもう少し,軌跡や通過領域を図形的に考えることが必要になり, それを述べたのが,「包絡線」である.
また,例題の(4)で,もし ![]() として対称性を崩すと,
たちまちこのままではできない.
この場合も領域の形を定めるためには,別の工夫がいる.
万能ということではなく,領域や軌跡が何によって定まるのかを,
しっかりおさえよ,ということである.
入試問題は,
この対象のなかにある論理がつかめているかを問う問題が多く,
したがって,ここで述べてきたことで解けるものがほとんどなのだ.
として対称性を崩すと,
たちまちこのままではできない.
この場合も領域の形を定めるためには,別の工夫がいる.
万能ということではなく,領域や軌跡が何によって定まるのかを,
しっかりおさえよ,ということである.
入試問題は,
この対象のなかにある論理がつかめているかを問う問題が多く,
したがって,ここで述べてきたことで解けるものがほとんどなのだ.
 例題 1.3
[92千葉大]
例題 1.3
[92千葉大]
線分ABを直径とする半円がある. 周上の弧PQを弦PQで折り返したとき,折り返された弧が ABに接したとする(右図). このような弦PQの存在する範囲を求めて図示せよ.
考え方
さてこれは何をどう置けばよいのか.
まずこれは座標平面に入れよう.当然円の中心を原点にする単位円だ.
座標平面に入れて考える.折り返すとはどういうことだ.
円弧を折り返すように考えるが,折り返された円弧は別の円の弧の一部だ.
 ここが飛躍だ.この新しい折り返された円は,当然もとの円と半径は同じ1だ.
では中心は.
ここが飛躍だ.この新しい折り返された円は,当然もとの円と半径は同じ1だ.
では中心は. ![]() 軸に接する円の中心の
軸に接する円の中心の ![]() 座標は
座標は ![]() 軸との接線だ.
そこで,「何をどう置くか」だ.
軸との接線だ.
そこで,「何をどう置くか」だ.
解答
接点を ![]() とおく.
折り返された円は中心が
とおく.
折り返された円は中心が ![]() で半径が1の円である.
で半径が1の円である.
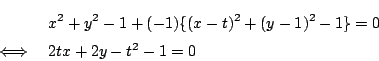
よって弦PQの通過範囲は
媒介変数 ![]() が
が
![]() を動くときの,
直線
を動くときの,
直線
![]() の通過範囲と,
円の周および内部の共通部分である.
の通過範囲と,
円の周および内部の共通部分である.
よって,
![]() ,
または
,
または
![]() 軸
軸 ![]() が成り立てばよい.
が成り立てばよい.
![]() がこの二組の条件のいずれにも入っているが,
「または」だからこれでよい.
がこの二組の条件のいずれにも入っているが,
「または」だからこれでよい.
これから次のいずれかを満たす点の集合と 円の周および内部との共通部分が求めるものである. 「,」はすべて「かつ」を意味する. \begin{eqnarray*} ①&&1-x-y\leqq 0,\ かつ\ 1+x-y\geqq 0\\ ②&&1-x-y\geqq 0,\ かつ\ 1+x-y\leqq 0\\ ③&&x^2-(1-2y)\geqq 0,\ 1-x-y\geqq 0,\ \\ &&\quad 1+x-y\geqq 0,\ かつ\ -1\le x\leqq 1 \end{eqnarray*}
この領域と半円の内部の共通部分が求める通過範囲である.
図示すると次のようになる.□
