


次: 積分法
上: 微分法
前: 連続関数
微分可能性については,連続性とはまったく様相が異なる.
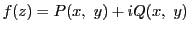 とすると,微分可能であるならば,
とすると,微分可能であるならば,
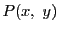 と
と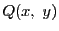 は互いに独立ではありえなくなる.
複素関数の連続性で定めたように,
は互いに独立ではありえなくなる.
複素関数の連続性で定めたように,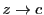 とは,
とは,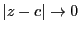 のこととする.
のこととする.
定義 1 (微分可能)
複素平面の領域
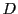
で定義された関数
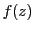
と
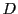
の点
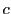
がある.
が存在するとき,関数
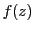
は
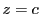
で微分可能である,という.
■
実数のなかでは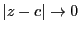 は2つの方向からの動きのみであるが、
複素平面上で
は2つの方向からの動きのみであるが、
複素平面上で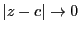 は,らせん状に動いたり,あらゆる方向からの動きがあり,
どのような動きに対しても収束するということが微分可能の条件である.
これは大変に強い条件である.
は,らせん状に動いたり,あらゆる方向からの動きがあり,
どのような動きに対しても収束するということが微分可能の条件である.
これは大変に強い条件である.
複素平面の領域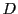 で定義された関数
で定義された関数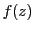 を,
を,
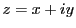 とし,
とし,
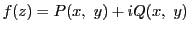 とおく.
また
とおく.
また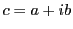 とする.
とする.
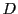 に対応する実2次元距離空間
に対応する実2次元距離空間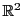 の領域も
の領域も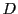 と書く.
と書く.
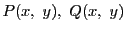 はそれぞれ
はそれぞれ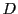 で定義された実数値関数である.
で定義された実数値関数である.
定理 2
領域
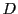
で定義された関数
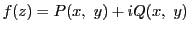
が,
領域
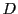
の点
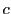
で微分可能であるための必要十分条件は,
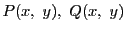
がそれぞれ
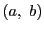
で微分可能(定義
![[*]](images/crossref.gif)
)で,
かつ
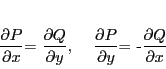 |
(1.1) |
が成り立つことである.
■
証明
関数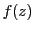 が
が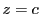 で微分可能であるとし,
で微分可能であるとし,
とおく.そして
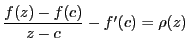 ,つまり
,つまり
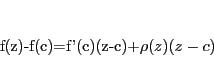 |
(1.2) |
とする.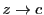 のとき
のとき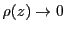 である.
さらに
である.
さらに
とおく.等式(1.2)を実部と虚部の等式にすると
となる.この等式は
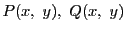 がそれぞれ
がそれぞれ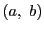 で微分可能で,
で微分可能で,
が成り立つ.つまり等式(1.1)が成り立つことを示している.
逆に
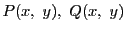 がそれぞれ
がそれぞれ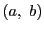 で微分可能(定義
で微分可能(定義![[*]](images/crossref.gif) )で,
かつ等式(1.1)が成り立つとする.
このとき,極限値
)で,
かつ等式(1.1)が成り立つとする.
このとき,極限値
が存在することを示す.
とおく.微分可能性と等式(1.1)から,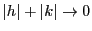 のとき,
のとき,
となる
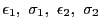 を用いて
を用いて
と表すことができる.これから
を得る.
つまり
となる.ここで
なので,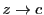 ,すなわち
,すなわち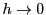 ,
,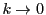 のとき
のとき
つまり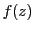 は
は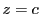 で微分可能である.
□
で微分可能である.
□
これで微分が定義され,微分可能性の条件が得られた.
この微分に関して,実関数の微分と同じように,2つの関数の四則の微分(定理![[*]](images/crossref.gif) ),合成関数,逆関数の微分(定理
),合成関数,逆関数の微分(定理![[*]](images/crossref.gif) )の計算定理が成り立つ.
)の計算定理が成り立つ.
関数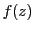 が
が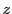 平面の領域
平面の領域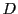 で定義され,複素平面上の曲線
で定義され,複素平面上の曲線
が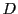 にふくまれているとする.
このとき,この曲線の
にふくまれているとする.
このとき,この曲線の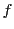 による像は
による像は
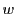 平面の曲線となる.それは
平面の曲線となる.それは
で与えられる.
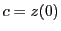 とし,曲線
とし,曲線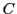 が点
が点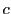 において接線を有するとする.
つまり
において接線を有するとする.
つまり
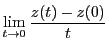 が存在するとする.
この接線と実軸とのなす角を
が存在するとする.
この接線と実軸とのなす角を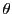 とすると.
とすると.
であるが,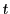 が正実数であり,
が正実数であり,
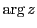 が三角関数の連続性より,
が三角関数の連続性より,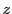 に関して連続であるので
に関して連続であるので
である.ここで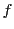 が
が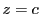 で微分可能で
で微分可能で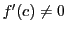 であるとする.
であるとする.
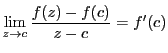 であるので,
偏角をとり
であるので,
偏角をとり
である.この結果,
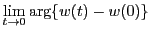 が存在し,この値を
が存在し,この値を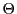 とすると,
とすると,
であることがわかる.
点 を2つの曲線
を2つの曲線
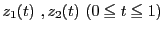 が通り,
が通り,
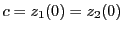 であるとし,それぞれの偏角の関係を
であるとし,それぞれの偏角の関係を
とすれば,
となり,2本の接線のなす角は,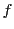 による写像によって不変に保たれることがわかる.
このような写像を等角写像という.改めて定義すると次のようになる.
による写像によって不変に保たれることがわかる.
このような写像を等角写像という.改めて定義すると次のようになる.
定義 3 (正則)
複素平面の領域
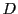
で定義された関数
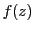
が,
領域のすべての点
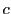
で微分可能であるとき,
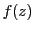
は
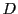
で
正則という.
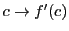
は
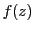
から導かれた関数となる.これを
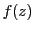
の
導関数といい,
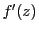
と表す.■
すで見たように,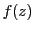 が
が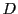 の各点で定理2を満たすことは,
の各点で定理2を満たすことは,
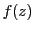 が
が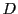 で正則である条件である.
で正則である条件である.
この定理にある条件の
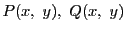 の
の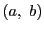 での微分可能(定義
での微分可能(定義![[*]](images/crossref.gif) )性は,
緩い条件である
)性は,
緩い条件である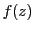 の連続性に置きかえても,同定理が成り立つ.
すなわち次の定理が成り立つ.
の連続性に置きかえても,同定理が成り立つ.
すなわち次の定理が成り立つ.
定理 3
関数
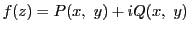
が
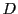
で正則であるための必要十分条件は,
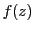
が
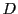
で連続で,
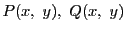
がそれぞれ
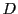
の可付番個の点を除いて偏微分可能で,
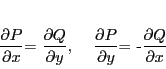 |
(1.3) |
が成り立つことである.
■
これはLooman-Menchoffの定理といわれているが,その証明には多くの準備が必要なので,
ここでは述べられない.
Subsections



次: 積分法
上: 微分法
前: 連続関数
Aozora
2020-04-17
![]() は2つの方向からの動きのみであるが、
複素平面上で
は2つの方向からの動きのみであるが、
複素平面上で![]() は,らせん状に動いたり,あらゆる方向からの動きがあり,
どのような動きに対しても収束するということが微分可能の条件である.
これは大変に強い条件である.
は,らせん状に動いたり,あらゆる方向からの動きがあり,
どのような動きに対しても収束するということが微分可能の条件である.
これは大変に強い条件である.
![]() で定義された関数
で定義された関数![]() を,
を,
![]() とし,
とし,
![]() とおく.
また
とおく.
また![]() とする.
とする.
![]() に対応する実2次元距離空間
に対応する実2次元距離空間![]() の領域も
の領域も![]() と書く.
と書く.
![]() はそれぞれ
はそれぞれ![]() で定義された実数値関数である.
で定義された実数値関数である.
![]() が
が![]() で微分可能であるとし,
で微分可能であるとし,
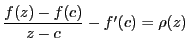 ,つまり
,つまり
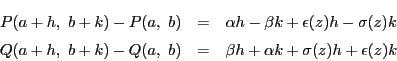
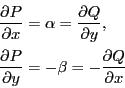
![]() がそれぞれ
がそれぞれ![]() で微分可能(定義
で微分可能(定義![[*]](images/crossref.gif) )で,
かつ等式(1.1)が成り立つとする.
このとき,極限値
)で,
かつ等式(1.1)が成り立つとする.
このとき,極限値
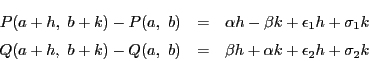
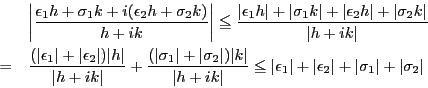
![[*]](images/crossref.gif) ),合成関数,逆関数の微分(定理
),合成関数,逆関数の微分(定理![[*]](images/crossref.gif) )の計算定理が成り立つ.
)の計算定理が成り立つ.
![]() とし,曲線
とし,曲線![]() が点
が点![]() において接線を有するとする.
つまり
において接線を有するとする.
つまり
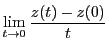 が存在するとする.
この接線と実軸とのなす角を
が存在するとする.
この接線と実軸とのなす角を![]() とすると.
とすると.
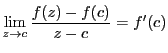 であるので,
偏角をとり
であるので,
偏角をとり
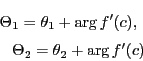
![]() が
が![]() の各点で定理2を満たすことは,
の各点で定理2を満たすことは,
![]() が
が![]() で正則である条件である.
で正則である条件である.
![]() の
の![]() での微分可能(定義
での微分可能(定義![[*]](images/crossref.gif) )性は,
緩い条件である
)性は,
緩い条件である![]() の連続性に置きかえても,同定理が成り立つ.
すなわち次の定理が成り立つ.
の連続性に置きかえても,同定理が成り立つ.
すなわち次の定理が成り立つ.