

 次: 積分計算
上: 積分の方法
前: 積分可能
次: 積分計算
上: 積分の方法
前: 積分可能
 が積分可能である区間で
が積分可能である区間で を定数,
を定数, を任意の点として
を任意の点として
とおくと,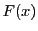 は同じ区間の関数になる.
は同じ区間の関数になる.
定理 53
関数

は閉区間
![$[a,\ b]$](images/img797.gif)
で有界である.
この区間内で関数
は連続である.
■
証明
区間で
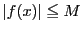 となる
となる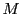 が存在する.
絶対値が十分小さい
が存在する.
絶対値が十分小さい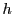 に対して
に対して
よって
となり,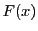 は連続である.
□
は連続である.
□
注意 5.4
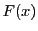
は連続ではあるけれども,必ずしも微分可能ではない.微分可能であることが保証される(つまり微分可能であるための十分条件)のは,

が連続な場合である.それが次定理である.
定理 54
関数

は閉区間
![$[a,\ b]$](images/img797.gif)
で連続である.
このとき,区間内の範囲の

に対し
が成り立つ.
■
証明
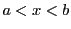 の範囲にある
の範囲にある に対し
に対し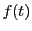 は区間
は区間![$[a,\ x]$](images/img1662.gif) でも積分可能なので,
でも積分可能なので,
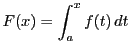 とおく.
区間
とおく.
区間 の2点
の2点 と
と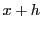 をとる.
をとる.
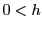 のとき定理60より
のとき定理60より
であるから,区間![$[x,\ x+h]$](images/img1666.gif) の分割
の分割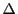 に対して
に対して
つまり
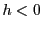 でも同様で,
でも同様で, は連続なので
は連続なので
よって,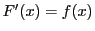 である.
□
である.
□
定義 26 (原始関数)
関数

が与えられたとき,

を導関数とする関数,つまり
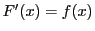
となる
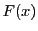
を

の
原始関数という.
■
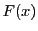 が
が の原始関数なら任意の定数
の原始関数なら任意の定数 に対して
に対して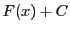 も
も の原始関数である.定理54は,
の原始関数である.定理54は, が連続関数なら
が連続関数なら
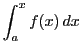 は
は の原始関数である,
つまり
の原始関数である,
つまり には原始関数が存在することを意味している.
には原始関数が存在することを意味している.
定義 27 (不定積分)
関数

が区間
![$[a,\ b]$](images/img797.gif)
で積分可能であるとき,
区間内の変数

に対する定積分
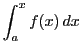
を,

の関数とみるとき,これを

の
不定積分という.
■
注意 5.5
定理
54によって,

の不定積分
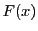
は

の原始関数である.
逆に, の任意の原始関数は,
の任意の原始関数は, のある不定積分と定数差を除いて一致する.
のある不定積分と定数差を除いて一致する.
昨今の高校数学では,このことを前提に,
関数 に対して
に対して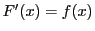 となる原始関数
となる原始関数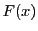 をとり,
これを用いて定積分を
をとり,
これを用いて定積分を
で定義する.
なお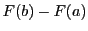 を
を
![$\Bigl[F(x) \Bigr]_a^b$](images/img1676.gif) のように記すことも多い.
のように記すことも多い.
不定積分
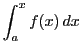 で,
で,
 を別の
を別の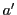 にかえると
にかえると
から
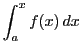 とは定数分だけ異なる.
とは定数分だけ異なる.
 を特に指定しないで
を特に指定しないで の関数として
の関数として
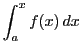 を考えると,
これは定数分を除いて定まる.
そこで,この関数を
を考えると,
これは定数分を除いて定まる.
そこで,この関数を
とのように書き,計算して結果に対して積分定数 をつけて,
定数分を除いて定まることを示すこともある.
をつけて,
定数分を除いて定まることを示すこともある.
これが現行の高校教科書の方法である.
函数 が区間
が区間![$[a,\ b]$](images/img797.gif) で有界,上限を
で有界,上限を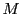 下限を
下限を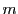 とする.
このとき
とする.
このとき
したがって
とくに が連続なら中間値の定理によって区間内に
が連続なら中間値の定理によって区間内に
となる が存在する.
が存在する.
 が連続という条件の下では
が連続という条件の下では の原始関数
の原始関数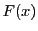 が存在するので,
微分の平均値の定理から
が存在するので,
微分の平均値の定理から
となる が存在する.
つまり微分の平均値の定理を原始関数に適用したものに他ならない
.これは次のように拡張される
が存在する.
つまり微分の平均値の定理を原始関数に適用したものに他ならない
.これは次のように拡張される
定理 55 (積分法の第一平均値定理)
函数

が区間
![$[a,\ b]$](images/img797.gif)
で連続,
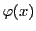
は積分可能で,
一定の符号を有する.このとき
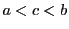
の

で
となるものが存在する.
■
定理 56 (積分法の第二平均値定理)
函数

が区間
![$[a,\ b]$](images/img797.gif)
で積分可能,
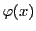
は有界で単調とする.
このとき区間内の

で
となるものが存在する.
■
これら二定理の証明は略する.
巾級数が表す関数には原始関数が存在する.
定理 57
関数

が収束半径
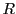
で巾級数
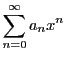
と展開されるとする.
このとき

には原始関数が存在し
で与えられる.
■
証明
 を
を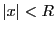 にとり,
にとり,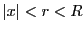 なる
なる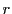 をとる.
をとる.
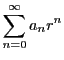 は収束するので
は収束するので
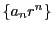 は有界である.
は有界である.
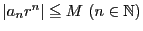 とする.
このとき,
巾級数
とする.
このとき,
巾級数
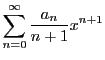 の項について
の項について
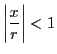 なので
級数
なので
級数
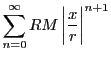 は
収束する.よって
は
収束する.よって
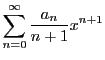 は絶対収束し,収束半径をもつ.
この関数を
は絶対収束し,収束半径をもつ.
この関数を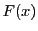 とする.
とする.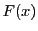 を項別に微分して得られる巾級数が
を項別に微分して得られる巾級数が であるから,
定理46
によって両者は同じ収束半径をもち,
であるから,
定理46
によって両者は同じ収束半径をもち,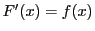 である.
□
である.
□


 次: 積分計算
上: 積分の方法
前: 積分可能
次: 積分計算
上: 積分の方法
前: 積分可能
2014-05-23
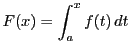 とおく.
区間
とおく.
区間![]() のとき定理60より
のとき定理60より
![]() でも同様で,
でも同様で,![]() は連続なので
は連続なので
![]() が
が![]() の原始関数なら任意の定数
の原始関数なら任意の定数![]() に対して
に対して![]() も
も![]() の原始関数である.定理54は,
の原始関数である.定理54は,![]() が連続関数なら
が連続関数なら
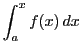 は
は![]() の原始関数である,
つまり
の原始関数である,
つまり![]() には原始関数が存在することを意味している.
には原始関数が存在することを意味している.
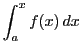 を,
を,
![]() に対して
に対して![]() となる原始関数
となる原始関数![]() をとり,
これを用いて定積分を
をとり,
これを用いて定積分を
![$\Bigl[F(x) \Bigr]_a^b$](images/img1676.gif) のように記すことも多い.
のように記すことも多い.
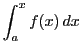 で,
で,
![]() を別の
を別の![]() にかえると
にかえると
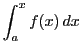 とは定数分だけ異なる.
とは定数分だけ異なる.
![]() を特に指定しないで
を特に指定しないで![]() の関数として
の関数として
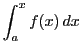 を考えると,
これは定数分を除いて定まる.
そこで,この関数を
を考えると,
これは定数分を除いて定まる.
そこで,この関数を
![]() が連続という条件の下では
が連続という条件の下では![]() の原始関数
の原始関数![]() が存在するので,
微分の平均値の定理から
が存在するので,
微分の平均値の定理から
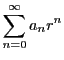 は収束するので
は収束するので
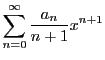 の項について
の項について
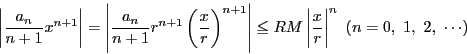
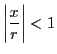 なので
級数
なので
級数
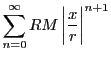 は
収束する.よって
は
収束する.よって
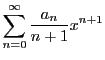 は絶対収束し,収束半径をもつ.
この関数を
は絶対収束し,収束半径をもつ.
この関数を