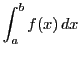 を原始関数の差
を原始関数の差
近年の高校数学では,![]() が負でない場合,
が負でない場合,![]() のグラフと
のグラフと![]() 軸および二直線
軸および二直線![]() で囲まれた図形の面積を
で囲まれた図形の面積を![]() とおくと,
とおくと,![]() となること,つまり
となること,つまり![]() が
が![]() の原始関数であることが解説される.一方,定積分
の原始関数であることが解説される.一方,定積分
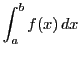 を原始関数の差
を原始関数の差![]() として定義する.その結果,定積分は
として定義する.その結果,定積分は![]() 軸とグラフとそして
軸とグラフとそして![]() 軸に平行な二本の直線で囲まれた領域の面積となる.唯一の数学的な内容は
軸に平行な二本の直線で囲まれた領域の面積となる.唯一の数学的な内容は![]() である.図形の面積に依拠して積分が定義されるということになっている.
である.図形の面積に依拠して積分が定義されるということになっている.
しかし実は定積分の定義は面積とは独立に,関数に固有のものとしてなされた.リーマン和もその極限も面積とは独立に定義され,計算できるときは計算された.そのため逆に,では定積分がどのような意味で面積なのかということが問題として浮かびあがってくる.この問題を最初に考えたのは,十九世紀末フランスの数学者ジョルダン(Marie Ennemond Camille Jordan、1838〜1922)ではないだろうか.ここではジョルダンによる面積の定義をふりかえり,定積分がこれとどのように結びつくのかを考えたい.
空間の部分集合に数を対応させる規則![]() がある.互いに共通部分をもたない部分集合の列
がある.互いに共通部分をもたない部分集合の列![]() があり,それぞれ値
があり,それぞれ値![]() は定まるとき,その和集合にも
は定まるとき,その和集合にも![]() の値が定まり次の等式が成り立つことを,加法性いう.
の値が定まり次の等式が成り立つことを,加法性いう.
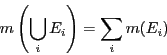
![]() の動く添え字の集合
の動く添え字の集合![]() はどのような範囲か.実は,有限集合にかぎる立場と,可算無限を許す立場がある.それがジョルダン測度とルベーグ測度である.共通なことは,距離が導入された空間の部分集合に,負でない実数を対応させる関数
はどのような範囲か.実は,有限集合にかぎる立場と,可算無限を許す立場がある.それがジョルダン測度とルベーグ測度である.共通なことは,距離が導入された空間の部分集合に,負でない実数を対応させる関数![]() で加法性をもつものを測度という.
で加法性をもつものを測度という.
測度論は,長さ,面積,体積,質量分布,確率分布などをとらえるための数学理論である.この問題を徹底して考えたのがフランスの数学者ルベーグ(Henri Lebesgue,1875〜1941)であった.1902年の論文『積分・長さおよび面積』で「測る」ということをとらえなおした.つまり![]() の構成から問題をとらえなおした.ルベーグ測度論である.そしてそのうえに積分論を再構築した.
の構成から問題をとらえなおした.ルベーグ測度論である.そしてそのうえに積分論を再構築した.
ここには,測ることにおいて,有限個の長方形で近似するところから,可算無限個の長方形で近似することへの飛躍があった.上の加法性を表す添え字![]() もまた,有限個から可算無限個に飛躍する.新しい現代解析学の基礎づけである.このような歴史をおさえておきたい.
もまた,有限個から可算無限個に飛躍する.新しい現代解析学の基礎づけである.このような歴史をおさえておきたい.
そのうえでわれわれの『解析基礎』はそれ以前,古典的な測度,ジョルダン測度の段階である.量を測るという観点からいえば,平面上の直線の長さと長方形の面積を与えられたものとして用いて,関数のグラフで囲まれた平面の部分集合の面積を,それに含まれる有限個の長方形の面積の上限と,それを含む有限個の長方形の面積の下限が一致するとき,その部分集合は「測れる」ものとし,その値を面積として定義する.
まず![]() 平面内の半開長方形
平面内の半開長方形
![]() で
で![]() に含まれるものと,
に含まれるものと,
![]() が
が![]() を含むものを考える.
を含むものを考える.

そこで
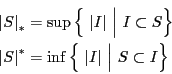
内部面積とは,
小さい長方形を加えていって
内から![]() を埋めていくときの上限である.
を埋めていくときの上限である.



![]() に含まれる長方形すべての和集合を
に含まれる長方形すべての和集合を![]() ,
,
![]() と共有点をもつすべての長方形の和集合を
と共有点をもつすべての長方形の和集合を![]() とする.
とする.
![]() と
と
![]() が存在するときは
が存在するときは
これは次のことから従う.
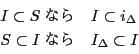

それはルベーグ測度に対して古典測度ともいうべきものである.
さてそこで問題はジョルダン測度の加法性である.
 一般に二つの長方形が共通部分をもつとき, この和集合を共通部分のない長方形の和に分けることができる.
一般に二つの長方形が共通部分をもつとき, この和集合を共通部分のない長方形の和に分けることができる.
したがって
![]() と一致する共通部分のない長方形の和を
と一致する共通部分のない長方形の和を![]() とすれば
とすれば![]() となる.
となる.
![]() を動かした下限をとることにより
を動かした下限をとることにより
各![]() は可測なので,
は可測なので,
このように有界な平面領域の可測性が定義された上は,定積分の可能性との関連が次のように明確になる.