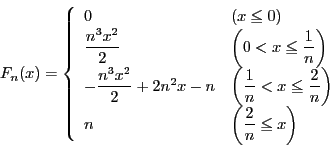関数![]() は区間
は区間![]() で連続であるとする.極限
で連続であるとする.極限
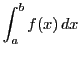 とする.
とする.
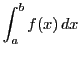 とする.
とする.
![]() や
や![]() のときも同様に考える.
つまりそれぞれの極限値が存在する場合,
のときも同様に考える.
つまりそれぞれの極限値が存在する場合,
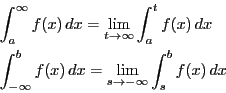
証明 条件から
証明
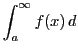 が存在する.
□
が存在する.
□
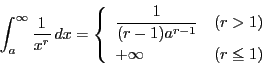
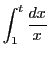 は発散する.
一方,
は発散する.
一方,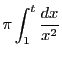 は収束する.
は収束する.
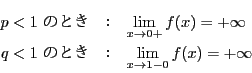
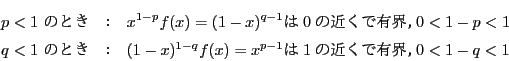
![]() のとき.ベータ関数の場合と同様に
のとき.ベータ関数の場合と同様に
次に,
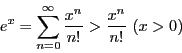
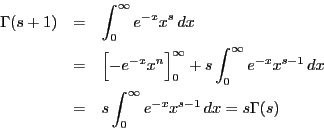
証明
![]() が一様収束することを示す.
そのためには
が一様収束することを示す.
そのためには
![]() がコーシー関数列(定義17)であることを示せばよい.
がコーシー関数列(定義17)であることを示せばよい.
![]() は
は![]() で一様収束するので,コーシー関数列である.
よって正数
で一様収束するので,コーシー関数列である.
よって正数![]() に対して自然数
に対して自然数![]() で,
で,
![]() なら
なら![]() の任意の
の任意の![]() に対して
に対して
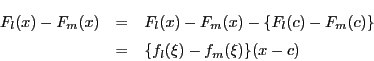
![]() であることは微分と関数列の定理である定理47
より従う.
□
であることは微分と関数列の定理である定理47
より従う.
□

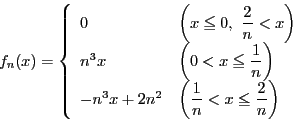
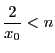 のとき
のとき
![]() に対し原始関数
に対し原始関数![]() を,
連続かつ
を,
連続かつ![]() になるように積分定数をとって構成する.
になるように積分定数をとって構成する.