

 次: 多次元積分
上: 次元の拡大
前: 多次元微分
次: 多次元積分
上: 次元の拡大
前: 多次元微分
定義 35
区間
![$I=[a,\ b]$](images/img1290.gif)
から
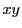
平面
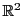
への写像を
平面曲線
という.
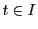
に対応する点
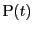
を,
二つの関数
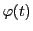
と
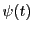
を用いて
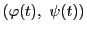
と表す.関数
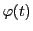
と
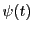
が連続であるとき

を
連続曲線という.
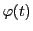
と
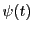
が微分可能であるとき

を
微分可能曲線という.
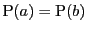 となる連続曲線を閉曲線という.
■
となる連続曲線を閉曲線という.
■
以下,混乱しないときは単に曲線という.
 は
は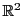 の点
の点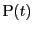 の集合
の集合
である.また変数と区間を明示するときは
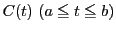 のようにも表すものとする.
これらの定義は,空間曲線についても同様である.
のようにも表すものとする.
これらの定義は,空間曲線についても同様である.
二点
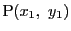 ,
,
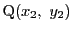 に対して線分
に対して線分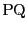 の長さが
の長さが
で定義されているとする.これをもとに,曲線の長さを定義しよう.
定義 36 (曲線の長さ)
区間

の分割を
とする.この分割を
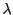
と書く.
 曲線
曲線 上の点
上の点
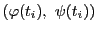 を
を
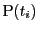 と表す.これによって2点
と表す.これによって2点
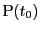 と
と
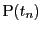 を端点とする折れ線
を端点とする折れ線
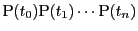 ができる.この長さを
ができる.この長さを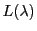 とする.
とする.
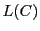
を
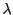
が区間
![$[a,\ b]$](images/img797.gif)
のすべての分割を(

も変化して)動くとき
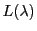
の上限
が存在すればそれを曲線

の長さと定義する.
■
分割の小区間
![$[t_{i-1},\ t_i]$](images/img2216.gif) をさらに分割して
をさらに分割して
![$[t_{i-1},\ s],\ [s,\ t_i]$](images/img2217.gif) とする.
三角形
とする.
三角形
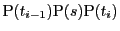 における三角不等式から
における三角不等式から
が成立する.したがって分割の細分に対して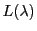 は単調に増加する.
は単調に増加する.
定理 76
閉区間
![$I=[a,\ b]$](images/img1290.gif)
と二つの関数
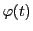
と
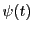
がある.
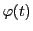
と
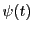
は区間
![$I=[a,\ b]$](images/img1290.gif)
を含むある開区間で微分可能で,
かつその導関数は区間

で連続である.さらに,
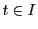
に対して
である.このとき曲線
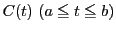
は長さ
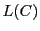
が定まり,
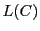
の値は
で与えられる.
■
証明
1.
折れ線の長さ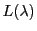 が有界であることを示す.
区間の分割
が有界であることを示す.
区間の分割 をとる.
をとる.
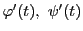 は閉区間で連続であるから有界で一様連続である.
区間
は閉区間で連続であるから有界で一様連続である.
区間 で
で
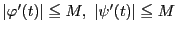 とする.
分割
とする.
分割 の小区間
の小区間
![$[t_i,\ t_{i+1}]$](images/img2224.gif) で平均値の定理を用いる.
この小区間内の点
で平均値の定理を用いる.
この小区間内の点
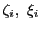 が存在して
が存在して
よって
よって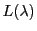 には上限が存在し,曲線
には上限が存在し,曲線 は長さ
は長さ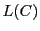 をもつ.
をもつ.
2.
次に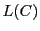 が定積分で与えられることを示す.
が定積分で与えられることを示す.
まず,
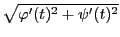 は連続であるから積分可能である.
は連続であるから積分可能である.
次に正数 を任意に定める.
を任意に定める.
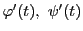 の一様連続性から
区間の任意の
の一様連続性から
区間の任意の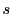 と
と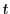 に対して
に対して
となる正数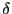 が存在する.
が存在する.
曲線の長さ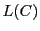 と定積分がそれぞれ存在するので,
分割を十分細かく,かついずれの小区間の幅も
と定積分がそれぞれ存在するので,
分割を十分細かく,かついずれの小区間の幅も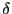 より小さくとって
より小さくとって
とすることができる.そこで
において第二の項を評価する.
一般に4実数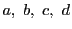 に対して次の不等式が成り立つ.
に対して次の不等式が成り立つ.
第一の不等式は三点
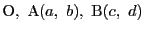 に対する三角不等式
に対する三角不等式
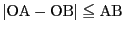 である.さらに両辺平方すれば明らかなように
である.さらに両辺平方すれば明らかなように
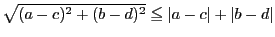 である.上記不等式はこれから従う.
である.上記不等式はこれから従う.
この結果,先の小区間での平均値の定理とあわせて
よって,
 は任意の正数なので
は任意の正数なので
が示された.
□
系 76.1
関数
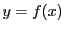
のグラフの
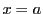
から
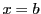
までの長さ
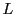
は
で与えられる.
■
証明
グラフは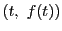 で表されるので,定理76より明らかである.
□
で表されるので,定理76より明らかである.
□
これによって円周の長さの存在が示される.
円は1点からの距離が一定であるような点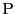 の集合である.
の集合である.
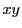 平面で考え中心が
平面で考え中心が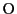 半径
半径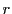 の
半円周上の点
の
半円周上の点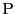 は
は
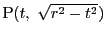 と表され,連続かつ微分可能である.したがって半円周の長さが存在することがわかる.
したがって円の弧長をもとにした三角関数も循環論法に陥ることなく定義される.
また,曲線の長さの定義から,
と表され,連続かつ微分可能である.したがって半円周の長さが存在することがわかる.
したがって円の弧長をもとにした三角関数も循環論法に陥ることなく定義される.
また,曲線の長さの定義から,
となる.このとき「外接する多角形の辺長の和の下限」も存在し円周の長さに一致することがわかる.
例 6.4 (放物線の弧長)
放物線
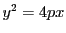
の頂点
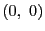
から点
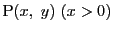
までの弧長を
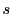
とおく.
放物線を
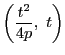
とすると
ここで
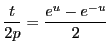
とおくと,
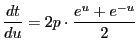
となる.また
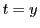
のとき
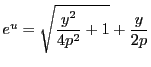
である.この
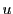
の値を

とする.
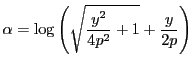
,
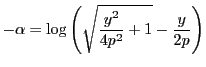
となる.
また
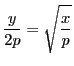
でもあるので
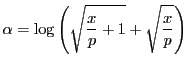
,
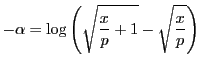
でもある.
例 6.5 (楕円の弧長)
楕円

を
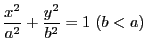
とする.
媒介変数では
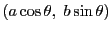
と表される.
点
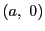
からの弧長を
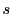
とすると
ここで
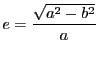
は離心率である.
この定積分は
楕円積分といわれ初等関数で表すことはできない.
本小節では の区間
の区間![$[a,\ b]$](images/img797.gif) から三次元ユークリッド空間
から三次元ユークリッド空間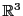 への関数
への関数 を考える.
を考える.
である. による区間の像を,三次元空間に置かれた曲線という.
による区間の像を,三次元空間に置かれた曲線という.
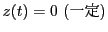 のときが平面曲線である.
のときが平面曲線である.
 によっては通常の曲線とはいえないものもできる.
これについては『解析概論』を見てほしい.
そこで次の二つの条件を加える.
によっては通常の曲線とはいえないものもできる.
これについては『解析概論』を見てほしい.
そこで次の二つの条件を加える.
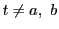 のとき
のとき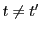 なら
なら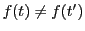 が成り立つ.
このような曲線を単一曲線,
あるいはジョルダン曲線という.
が成り立つ.
このような曲線を単一曲線,
あるいはジョルダン曲線という.
-
![$t\ \in [a,\ b]$](images/img2269.gif) に対し
に対し
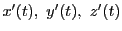 が存在し,
が存在し,
が成り立つ.
これを滑らかな曲線という.
このような曲線を解析するためには,ベクトルの微分が必要である.
空間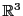 の要素であるベクトルには内積と外積が定められる.
これらと微分との関連を整理する.
この部分は曲線や曲面の微分法による解析,あるいは曲面上の微積,という方向に発展していく.それが微分幾何学である.ここでは当面の必要に従い内積と外積を定義しその微分を考え,曲率等の基本事項をまとめるにとどめる.
の要素であるベクトルには内積と外積が定められる.
これらと微分との関連を整理する.
この部分は曲線や曲面の微分法による解析,あるいは曲面上の微積,という方向に発展していく.それが微分幾何学である.ここでは当面の必要に従い内積と外積を定義しその微分を考え,曲率等の基本事項をまとめるにとどめる.
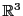 では,その要素
では,その要素
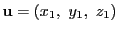 に対し,大きさを
に対し,大きさを
が定まっている.これを用いて
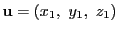 ,
,
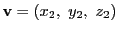 に対して内積が定義される.
に対して内積が定義される.
を
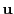 と
と
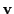 の内積とする.
内積はまたスカラー積ともいう.
「
の内積とする.
内積はまたスカラー積ともいう.
「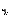 」を略して
」を略して
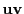 と書くこともあれば,
と書くこともあれば,
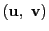 のように書くこともある.
これに関することは『線型代数の考え方』−「ベクトル空間と線型写像」−「内積とベクトルの大きさ」を見てほしい.
のように書くこともある.
これに関することは『線型代数の考え方』−「ベクトル空間と線型写像」−「内積とベクトルの大きさ」を見てほしい.
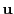 と
と
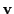 の間の角を
の間の角を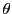 とすれば,
とすれば,
となる.特に
である.
ベクトル
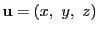 の各成分が実数
の各成分が実数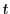 の関数であるとき,
ベクトル
の関数であるとき,
ベクトル
を
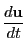 あるいは
あるいは
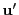 と書き表すことにする.
と書き表すことにする.
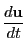 も
も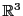 に値をとる関数となる.
二つのベクトル
に値をとる関数となる.
二つのベクトル
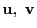 の各成分がそれぞれ
の各成分がそれぞれ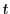 の関数のとき
の関数のとき
が成り立つ.
特に
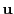 が方向のみ変化して,つねに大きさが1のとき,
つまり
が方向のみ変化して,つねに大きさが1のとき,
つまり
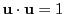 のとき,
のとき,
となる.この場合
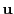 と
と
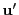 は直交している.
は直交している.
二つのベクトル
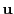 と
と
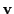 があり,その成分を
があり,その成分を
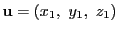 ,
,
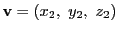 とする.
ベクトル
とする.
ベクトル
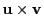 を
を
で定め,
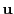 と
と
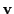 の外積という.
ベクトル積ともいう.
の外積という.
ベクトル積ともいう.
同様に,
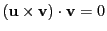 も成り立つ.
よって
も成り立つ.
よって
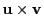 は
は
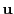 と
と
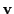 の双方に直交している.
の双方に直交している.
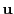 と
と
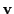 のなす角を
のなす角を
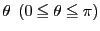 とおく.
とおく.
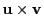 の大きさは
それぞれの大きさとなす角
の大きさは
それぞれの大きさとなす角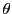 のみで決まる.
双方に直交しているので,方向が決まれば図形的性質が確定する.
のみで決まる.
双方に直交しているので,方向が決まれば図形的性質が確定する.
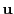 と
と
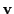 を連続的に回転し,
を連続的に回転し,
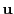 が
が 軸上に
軸上に
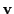 が
が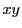 平面上にあるように置く.
この回転で
平面上にあるように置く.
この回転で
となったとする.
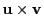 も連続的に変化するので,
も連続的に変化するので,
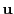 と
と
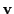 との位置関係は変わらない.
このとき外積は
との位置関係は変わらない.
このとき外積は
となり,
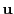 から
から
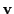 へ右ネジを回したときの進む方向になっている.
よって
へ右ネジを回したときの進む方向になっている.
よって
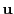 から
から
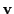 の外積
の外積
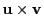 は,
ベクトル
は,
ベクトル
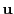 からベクトル
からベクトル
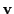 へ右ネジを回転させたとき,
ネジの進む方向であることがわかる.
へ右ネジを回転させたとき,
ネジの進む方向であることがわかる.
注意 6.4
三次の行列式を用いて平行六面体の向きつき体積の考察を行っておくと,
もう少し簡明な議論をすることができる.これについても『解析概論』など参照してほしい.
外積は次のような計算法則を満たす.
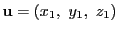 と
と
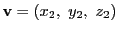 の各成分が
の各成分が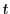 の関数のとき,
の関数のとき,
を考えると, 成分についてみれば
成分についてみれば
となる.他の成分についても同様なので,
が成り立つ.
関数 で定まる滑らかな空間曲線を
で定まる滑らかな空間曲線を とする.
とする.
 は
は
という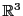 の部分集合である.
の部分集合である.
 上の点の位置ベクトルを
上の点の位置ベクトルを
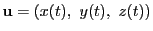 とする.
以上の準備のもと,空間曲線の局所的な性質について考える.
とする.
以上の準備のもと,空間曲線の局所的な性質について考える.
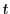 は一般的な媒介変数である.
は一般的な媒介変数である. をそのままに,媒介変数
をそのままに,媒介変数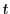 を別の変数に置換することを考える.
新しい媒介変数として,曲線の始点
を別の変数に置換することを考える.
新しい媒介変数として,曲線の始点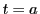 からの距離
からの距離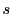 をとる.
空間曲線においても平面曲線の長さと同様に,
をとる.
空間曲線においても平面曲線の長さと同様に,
である.この で
で を表す.
を表す.
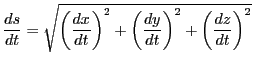 であるから
であるから
である. による微分と区別するために
による微分と区別するために
 による微分を
による微分を
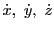 とし,
とし,
と書く.ここのところの記号は『解析概論』と違うので注意してほしい.
この等式は
を意味する.するとベクトル
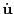 は単位ベクトルである.
従って,ベクトル
は単位ベクトルである.
従って,ベクトル
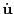 とその微分
とその微分
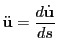 は直交している.
は直交している.
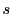 に対応する点を
に対応する点を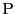 とする.
とする.
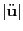 の値を曲線
の値を曲線 の
点
の
点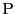 における曲率といい
における曲率といい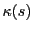 と置く.
その逆数を曲率半径という.
と置く.
その逆数を曲率半径という.
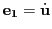 とし,これに平行な直線を主法線,
とし,これに平行な直線を主法線,
 を含む平面を接触平面という.
次に
を含む平面を接触平面という.
次に
 に平行な単位ベクトル
に平行な単位ベクトル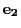 を
を
で定める.さらに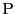 における接触平面の垂線と平行な単位ベクトル
における接触平面の垂線と平行な単位ベクトル
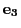 を
を
で定める.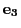 で定まる接触平面の垂線
を従法線という.
すると,
で定まる接触平面の垂線
を従法線という.
すると,
ゆえに
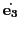 は
は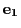 に垂直である.
に垂直である.
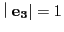 より
より
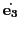 は
は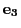 に垂直.つまり
に垂直.つまり
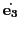 は
は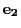 に平行である.ここで
に平行である.ここで
とおいて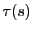 を曲線
を曲線 の第二曲率または捩率といい,
その逆数を捩率半径という.
の第二曲率または捩率といい,
その逆数を捩率半径という.
従って
以上の定数を用いると,
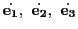 を
を
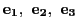 を用いて表すことができる.
を用いて表すことができる.
これをフルネ・セレーの公式という.
例 6.6
常螺旋(heilix)は次のように定義される.
より
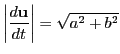
なので
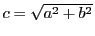
とおき
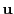
を
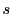
で表すと
よって
常螺旋では曲率
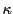
も捩率
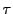
も定数になる.
ここから、空間曲線の大域的な理論,空間曲面の局所理論,大域理論へと進むのであるが,
それが微分幾何学である.『解析基礎』としてはここでおかねばならないが,
最後に平面曲線の場合の曲率についてよく知られた公式と関係を見ておこう.
平面曲線は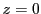 に固定した場合である.空間曲線では曲率を非負にとり,捩率を符号をもつ量とした.平面曲線の場合は,曲率段階で符号を決めることができる.
に固定した場合である.空間曲線では曲率を非負にとり,捩率を符号をもつ量とした.平面曲線の場合は,曲率段階で符号を決めることができる.
接線ベクトル
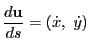 が
が 軸の正の方向となす角を
軸の正の方向となす角を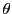 とする.
とする.
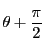 方向の単位ベクトルを
方向の単位ベクトルを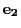 にとる.
このとき曲率
にとる.
このとき曲率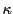 を
を
とする.
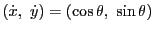 であるから
であるから
となる.つまり
である.
これは,曲線の長さを媒介変数に取ったときである.一般の媒介変数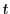 で曲率はどのようになるか.
で曲率はどのようになるか.
この二式から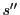 を消去する.
を消去する.
ここで
を代入し,
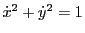 を用いると
を用いると
を得る.
曲線が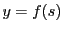 という明示的な関数のグラフである場合.
曲線
という明示的な関数のグラフである場合.
曲線 は
は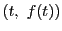 となるので,
となるので,
となる.
例 6.7
指数螺旋
の曲率を求める.
なので
である.
平面曲線に関しても伸開線,縮閉線の話題や,包絡線の一般論などさまざまに論ずべきことがあるが,ここは当初の目的である力学の数学的な基礎部分に絞ってここで終え,次に進まなければならない.


 次: 多次元積分
上: 次元の拡大
前: 陰関数定理
次: 多次元積分
上: 次元の拡大
前: 陰関数定理
2014-05-23
![]() となる連続曲線を閉曲線という.
■
となる連続曲線を閉曲線という.
■
![]() となる連続曲線を閉曲線という.
■
となる連続曲線を閉曲線という.
■
![]() は
は![]() の点
の点![]() の集合
の集合
 曲線
曲線![]() 上の点
上の点
![]() を
を
![]() と表す.これによって2点
と表す.これによって2点
![]() と
と
![]() を端点とする折れ線
を端点とする折れ線
![]() ができる.この長さを
ができる.この長さを![]() とする.
とする.
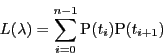
![]() をさらに分割して
をさらに分割して
![]() とする.
三角形
とする.
三角形
![]() における三角不等式から
における三角不等式から
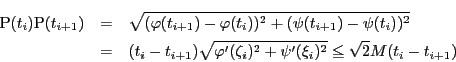
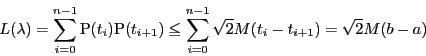
![]() は連続であるから積分可能である.
は連続であるから積分可能である.
![]() を任意に定める.
を任意に定める.
![]() の一様連続性から
区間の任意の
の一様連続性から
区間の任意の![]() と
と![]() に対して
に対して
![]() と定積分がそれぞれ存在するので,
分割を十分細かく,かついずれの小区間の幅も
と定積分がそれぞれ存在するので,
分割を十分細かく,かついずれの小区間の幅も![]() より小さくとって
より小さくとって
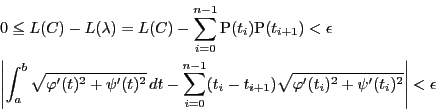
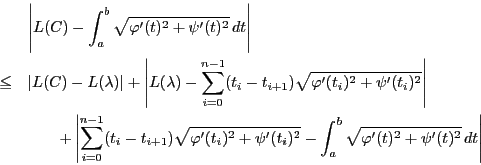
![]() に対して次の不等式が成り立つ.
に対して次の不等式が成り立つ.
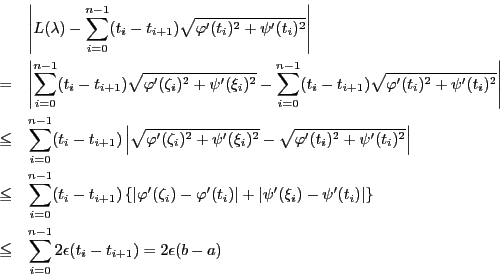
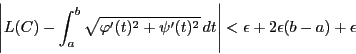
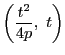 とすると
とすると
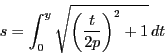
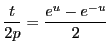 とおくと,
とおくと,
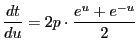 となる.また
となる.また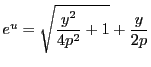 である.この
である.この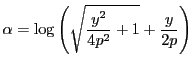 ,
,
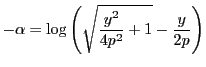 となる.
また
となる.
また
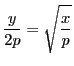 でもあるので
でもあるので
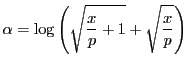 ,
,
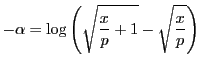 でもある.
でもある.
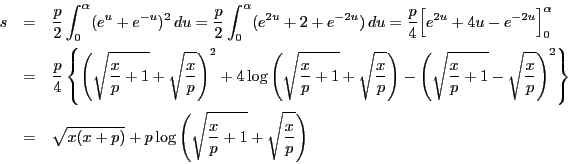
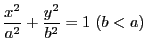 とする.
媒介変数では
とする.
媒介変数では
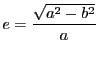 は離心率である.
この定積分は楕円積分といわれ初等関数で表すことはできない.
は離心率である.
この定積分は楕円積分といわれ初等関数で表すことはできない.
![]() の要素であるベクトルには内積と外積が定められる.
これらと微分との関連を整理する.
この部分は曲線や曲面の微分法による解析,あるいは曲面上の微積,という方向に発展していく.それが微分幾何学である.ここでは当面の必要に従い内積と外積を定義しその微分を考え,曲率等の基本事項をまとめるにとどめる.
の要素であるベクトルには内積と外積が定められる.
これらと微分との関連を整理する.
この部分は曲線や曲面の微分法による解析,あるいは曲面上の微積,という方向に発展していく.それが微分幾何学である.ここでは当面の必要に従い内積と外積を定義しその微分を考え,曲率等の基本事項をまとめるにとどめる.
![]() と
と
![]() の間の角を
の間の角を![]() とすれば,
とすれば,
![]() の各成分が実数
の各成分が実数![]() の関数であるとき,
ベクトル
の関数であるとき,
ベクトル
![]() と
と
![]() のなす角を
のなす角を
![]() とおく.
とおく.
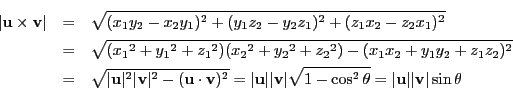
![]() と
と
![]() を連続的に回転し,
を連続的に回転し,
![]() が
が![]() 軸上に
軸上に
![]() が
が![]() 平面上にあるように置く.
この回転で
平面上にあるように置く.
この回転で
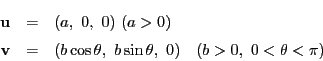
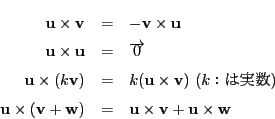
![]() は一般的な媒介変数である.
は一般的な媒介変数である.![]() をそのままに,媒介変数
をそのままに,媒介変数![]() を別の変数に置換することを考える.
新しい媒介変数として,曲線の始点
を別の変数に置換することを考える.
新しい媒介変数として,曲線の始点![]() からの距離
からの距離![]() をとる.
空間曲線においても平面曲線の長さと同様に,
をとる.
空間曲線においても平面曲線の長さと同様に,
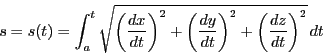
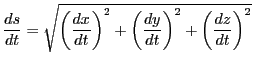 であるから
であるから
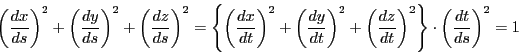
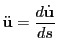 は直交している.
は直交している.
![]() に対応する点を
に対応する点を![]() とする.
とする.
![]() の値を曲線
の値を曲線![]() の
点
の
点![]() における曲率といい
における曲率といい![]() と置く.
その逆数を曲率半径という.
と置く.
その逆数を曲率半径という.
![]() とし,これに平行な直線を主法線,
とし,これに平行な直線を主法線,
![]() を含む平面を接触平面という.
次に
を含む平面を接触平面という.
次に
![]() に平行な単位ベクトル
に平行な単位ベクトル![]() を
を
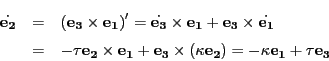
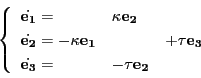
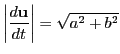 なので
なので
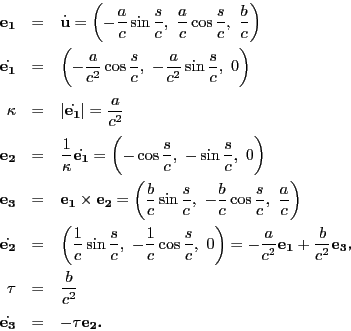
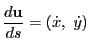 が
が![]() 軸の正の方向となす角を
軸の正の方向となす角を![]() とする.
とする.
![]() 方向の単位ベクトルを
方向の単位ベクトルを![]() にとる.
このとき曲率
にとる.
このとき曲率![]() を
を
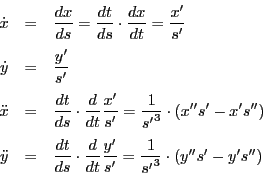
![]() という明示的な関数のグラフである場合.
曲線
という明示的な関数のグラフである場合.
曲線![]() は
は![]() となるので,
となるので,
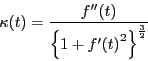
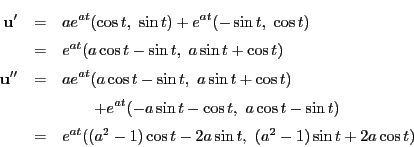
![\begin{eqnarray*}
x'y''-x''y'&=&e^{2at}
\left[(a\cos t-\sin t)\{(a^2-1)\sin t+...
...in t+\cos t)\{(a^2-1)\cos t-2a\sin t\} \right]
=(a^2+1)e^{2at}
\end{eqnarray*}](images/img2359.gif)