次: 微分と幾何
上: 次元の拡大
前: 不動点定理
次: 微分と幾何
上: 次元の拡大
前: 不動点定理
以下では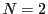 とし,平面
とし,平面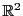 の部分集合
の部分集合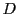 で定義された関数
で定義された関数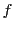 を考える.
これを
を考える.
これを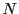 次元に一般化することは難しいことではないが,ときには
次元に一般化することは難しいことではないが,ときには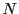 次の線型代数を必要とする.
次の線型代数を必要とする.
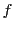 の従属変数を
の従属変数を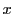 と
と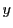 にとり
にとり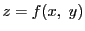 のように表す.
のように表す.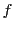 が連続な場合,
が連続な場合,
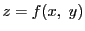 によって
によって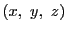 を座標系とする三次元空間
を座標系とする三次元空間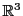 に置かれた曲面が定まる.
に置かれた曲面が定まる.
定義領域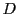 の点
の点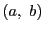 をとる.
をとる.
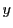 を
を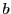 に固定し
に固定し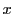 の関数としての
の関数としての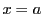 における微分係数が存在するときそれを
における微分係数が存在するときそれを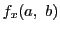 と書き,
と書き,
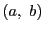 における
における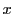 についての偏微分係数という.
についての偏微分係数という.
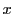 を
を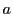 に固定し
に固定し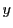 の関数としての
の関数としての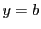 における微分係数が存在するときそれを
における微分係数が存在するときそれを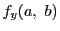 と書き,
と書き,
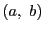 における
における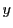 についての偏微分係数という.
についての偏微分係数という.
である.
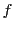 が
が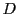 の各点で
の各点で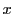 についての偏微分係数をもつとき,
についての偏微分係数をもつとき,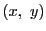 にその偏微分係数値を対応させる関数を
にその偏微分係数値を対応させる関数を
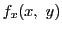 と書き,
と書き,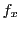 を
を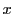 についての偏導関数という.
についての偏導関数という.
などと書く.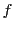 が
が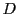 の各点で
の各点で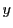 についての偏微分係数をもつとき,
についての偏微分係数をもつとき,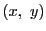 にその偏微分係数値を対応させる関数を
にその偏微分係数値を対応させる関数を
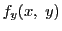 と書き,
と書き,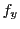 を
を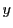 についての偏導関数という.
についての偏導関数という.
などと書く.
偏微分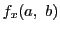 は,
は,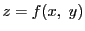 で定まる曲面を
で定まる曲面を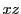 平面に平行な平面
平面に平行な平面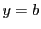 で切った断面上の曲線上の点
で切った断面上の曲線上の点
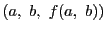 での接線の傾きを表す.
での接線の傾きを表す.
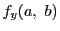 についても同様である.
これはまだ
についても同様である.
これはまだ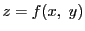 の微分可能性を特徴づけたものではない.
の微分可能性を特徴づけたものではない.
一変数の場合の微分係数を顧みる.
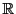 の区間で定義された関数
の区間で定義された関数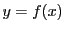 の
の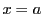 における微分係数
における微分係数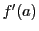 とは,
とは,
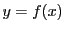 のグラフである曲線の点
のグラフである曲線の点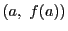 における接線の傾きであり,
における接線の傾きであり,
が接線の方程式であった.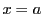 における微分可能性とは,
点
における微分可能性とは,
点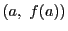 における接線の存在に他ならなかった.
いいかえると
における接線の存在に他ならなかった.
いいかえると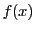 の
の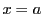 における微分可能性とは
における微分可能性とは
となる(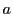 のみによる)定数
のみによる)定数 の存在と同値である.
これを二変数の場合に拡張する.
の存在と同値である.
これを二変数の場合に拡張する.
定義 34 (微分可能)
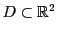
の変数で定義された関数
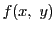
と
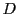
の点
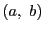
に対し,
となる(
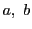
のみによる)定数
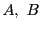
が存在
するとき,
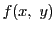
は点
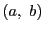
で
微分可能であるという.
関数
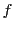
が
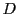
の各点で微分可能なとき
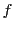
は
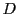
において微分可能であるという.
■
定義34の条件は次の表現と同値である.
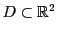 の変数を
の変数を
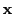 ,
定点を
,
定点を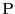 とする.
とする.
となるベクトル
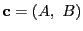 が存在する.ただし,
が存在する.ただし,
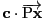 は内積を表す.
■
は内積を表す.
■
注意 6.2
本定義における「微分可能」を全微分可能ということも多い.
ここは『解析概論』の用語に従った.
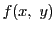 が点
が点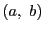 で微分可能であるとする.
で微分可能であるとする.
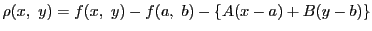 とおくと
とおくと
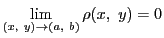 なので,
なので,
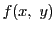 は点
は点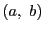 で連続である.さらに,
で連続である.さらに,
なので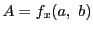 ,同様に
,同様に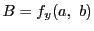 である.一次式
である.一次式
を全微分,平面
を曲面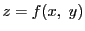 の点
の点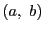 における接平面という.
における接平面という.
定理 74
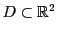
で定義された関数
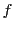
が偏導関数
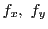
をもち,
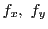
が
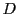
で連続ならば,
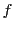
は
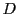
において微分可能である.
■
証明
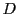 の点
の点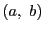 をとり
をとり
とおく.一変数の平均値の定理によって
と表される.よって
となる.
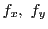 は連続なので,正数
は連続なので,正数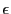 に対し
に対し
となる正数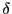 が存在する.よって
が存在する.よって
つまり
ゆえに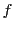 は
は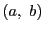 で微分可能.
で微分可能.
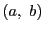 は
は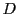 の任意の点であるから,
の任意の点であるから,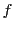 は
は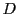 で微分可能である.
□
で微分可能である.
□
注意 6.3
本定理は
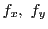
の存在と,いずれか一方の連続性のみを仮定すれば成立する.
これについては『解析概論』
定理26を参照のこと.
系 74.1
領域
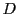
で関数
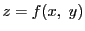
が微分可能であるとする.
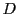
内の微分可能な曲線
![$C:(\varphi(t),\ \psi(t)),\ t\in [a,\ b]$](images/img2132.gif)
がある.
関数
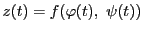
に関して
が成り立つ.
■
証明
記号は定理74を用いる.
区間![$[a,\ b]$](images/img797.gif) 内の点
内の点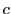 をとる.
をとる.
と表せる.ここで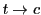 のとき
のとき
となる.よって
である.
これが任意の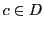 で成立するので命題が示された.
□
で成立するので命題が示された.
□
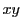 平面の開集合
平面の開集合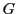 で定義された連続関数
で定義された連続関数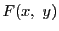 がある.
がある.
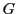 の点
の点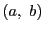 で
で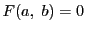 であるとする.
このとき,
であるとする.
このとき,
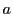 を含む実数のある開区間
を含む実数のある開区間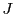 で定義された連続関数
で定義された連続関数
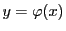 で
で
を満たすものを,
方程式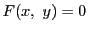 が定める陰関数という.
が定める陰関数という.
陰関数の存在に関して,次の定理が成り立つ.
定理 75 (陰関数定理)
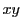
平面の開集合
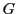
で定義された連続関数
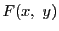
がある.
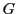
の点
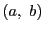
で
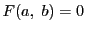
であり,かつ
である.このとき,
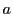
を含むある開区間
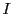
で連続で,
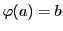
かつ
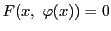
となる関数
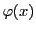
がただ一つ存在する.
さらに,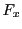 が連続なら
が連続なら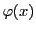 は微分可能で
は微分可能で
となる.
■
証明
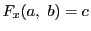 とし,
とし,
とおく.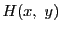 は次の条件を満たしている.
は次の条件を満たしている.
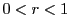 をとる.
をとる.
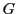 が開集合であり,
が開集合であり,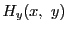 が
が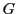 で連続で
で連続で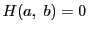 なので,
なので,
をとり,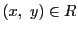 に対して
に対して
となる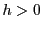 ,
,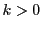 が存在する.
さらに
が存在する.
さらに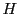 が連続で
が連続で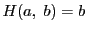 なので,
なので,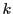 を十分小さく,
を十分小さく,
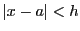 のとき
のとき
となるように,とることができる.
平均値の定理から
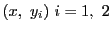 に対し
に対し
である.よって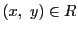 に対し
に対し
となる.
次に閉区間![$I=[a-h,\ a+h]$](images/img2168.gif) での連続関数空間
での連続関数空間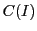 において,
において,
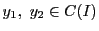 に対して,
距離を
に対して,
距離を
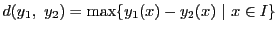 で定める.そして部分空間
で定める.そして部分空間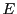 を
を
にとると,距離空間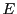 は
は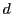 に関して完備である.
に関して完備である.
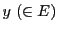 に対して
に対して
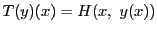 とおく.
とおく.
であるから,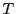 は
は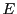 から
から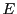 への写像である.
への写像である.
さらに,
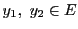 に対して,
に対して,
である.よって
が成り立ち,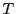 は縮小写像である.
は縮小写像である.
不動点定理72によって,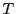 はただ一つの不動点をもつ.
それを
はただ一つの不動点をもつ.
それを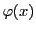 とすると,
とすると,
が成り立つ.つまり
である.
条件を満たす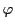 は
は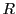 の関数としてただ一つである.
つまり,
の関数としてただ一つである.
つまり,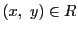 で
で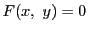 であるとするとき,
であるとするとき,
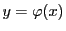 が成り立つ.次のように示される.
が成り立つ.次のように示される.
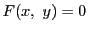 より
より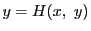 なので,
なので,
が成り立つ.
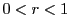 より
より
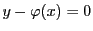 .つまり
.つまり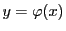 が成り立つ.
とくに,
が成り立つ.
とくに,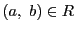 で
で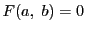 なので
なので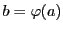 である.
である.
さらに,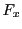 も連続なら定理74によって
も連続なら定理74によって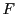 は全微分可能である.
よって
は全微分可能である.
よって
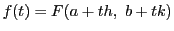 について,
区間
について,
区間![$[0,\ 1]$](images/img1498.gif) で平均値の定理を用いることにより,
その系74.1から
で平均値の定理を用いることにより,
その系74.1から
である.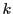 を
を
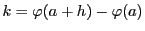 にとると,
にとると,
なので,
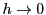 をとって
をとって
を得る.
□
系 75.1
関数
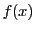
が開区間で微分可能で,
その区間内の
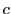
で
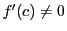
であり,
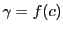
なら,
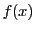
は
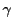
を含む開区間で定義された逆関数
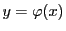
をもつ.
そして,
となる.
■
証明
とおく.
であるから,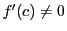 のとき陰関数
のとき陰関数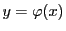 が存在し,
が存在し,
である.
さらに
なので,
である.
□


 次: 微分と幾何
上: 次元の拡大
前: 不動点定理
次: 微分と幾何
上: 次元の拡大
前: 不動点定理
2014-05-23
![]() の点
の点![]() をとる.
をとる.
![]() を
を![]() に固定し
に固定し![]() の関数としての
の関数としての![]() における微分係数が存在するときそれを
における微分係数が存在するときそれを![]() と書き,
と書き,
![]() における
における![]() についての偏微分係数という.
についての偏微分係数という.
![]() を
を![]() に固定し
に固定し![]() の関数としての
の関数としての![]() における微分係数が存在するときそれを
における微分係数が存在するときそれを![]() と書き,
と書き,
![]() における
における![]() についての偏微分係数という.
についての偏微分係数という.
![]() が
が![]() の各点で
の各点で![]() についての偏微分係数をもつとき,
についての偏微分係数をもつとき,![]() にその偏微分係数値を対応させる関数を
にその偏微分係数値を対応させる関数を
![]() と書き,
と書き,![]() を
を![]() についての偏導関数という.
についての偏導関数という.
![]() の区間で定義された関数
の区間で定義された関数![]() の
の![]() における微分係数
における微分係数![]() とは,
とは,
![]() のグラフである曲線の点
のグラフである曲線の点![]() における接線の傾きであり,
における接線の傾きであり,
![]() の変数を
の変数を
![]() ,
定点を
,
定点を![]() とする.
とする.
![]() が点
が点![]() で微分可能であるとする.
で微分可能であるとする.
![]() とおくと
とおくと
![]() なので,
なので,
![]() は点
は点![]() で連続である.さらに,
で連続である.さらに,
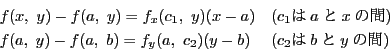
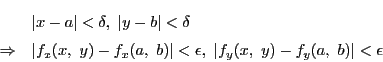
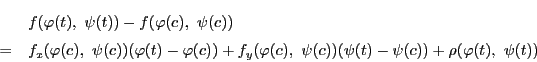
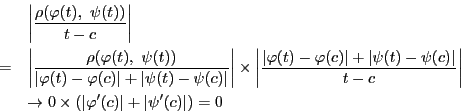
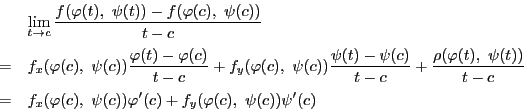
![]() が連続なら
が連続なら![]() は微分可能で
は微分可能で
![]() をとる.
をとる.
![]() が開集合であり,
が開集合であり,![]() が
が![]() で連続で
で連続で![]() なので,
なので,
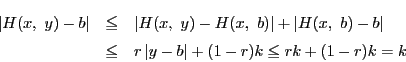
![]() での連続関数空間
での連続関数空間![]() において,
において,
![]() に対して,
距離を
に対して,
距離を
![]() で定める.そして部分空間
で定める.そして部分空間![]() を
を
![]() に対して
に対して
![]() とおく.
とおく.
![]() に対して,
に対して,
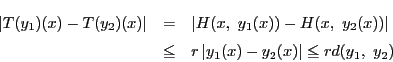
![]() はただ一つの不動点をもつ.
それを
はただ一つの不動点をもつ.
それを![]() とすると,
とすると,
![]() は
は![]() の関数としてただ一つである.
つまり,
の関数としてただ一つである.
つまり,![]() で
で![]() であるとするとき,
であるとするとき,
![]() が成り立つ.次のように示される.
が成り立つ.次のように示される.
![]() より
より![]() なので,
なので,
![]() も連続なら定理74によって
も連続なら定理74によって![]() は全微分可能である.
よって
は全微分可能である.
よって
![]() について,
区間
について,
区間![]() で平均値の定理を用いることにより,
その系74.1から
で平均値の定理を用いることにより,
その系74.1から