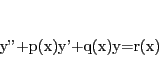次: 惑星の運動
上: 微分方程式
前: 解の存在定理
次: 惑星の運動
上: 微分方程式
前: 解の存在定理
二階線形微分方程式の解の存在と解の構造についてまとめよう.
まず,二階線形微分方程式の解の存在を示そう.
方針は一階正規形の場合と同様に,
微分方程式と初期条件を一つの積分方程式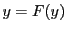 に還元し,
に還元し,
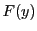 が縮小写像であるようにとれることを示し,解の存在を示す.
初期条件が複雑な分だけ
が縮小写像であるようにとれることを示し,解の存在を示す.
初期条件が複雑な分だけ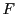 の構成が複雑である.
の構成が複雑である.
定理 85
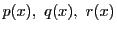
を実数
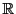
で定義された連続な関数とする.
二階線形微分方程式
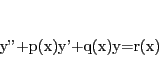 |
(8) |
の解で,初期条件
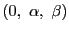
を満たす,つまり
となるものが一意に存在する.
■
証明
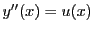 とおく.
とおく.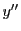 についての初期条件はないので,
これをもとに初期条件を満たす
についての初期条件はないので,
これをもとに初期条件を満たす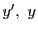 を構成する.
を構成する.
これらが微分方程式を満たすように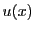 が決定できればよい.
積分変数をそろえて微分方程式に代入する.
が決定できればよい.
積分変数をそろえて微分方程式に代入する.
そこで
とおくと
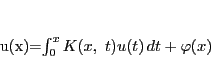 |
(9) |
となる.これを満たす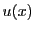 が一意に存在することを示せばよい.
が一意に存在することを示せばよい.
任意の正数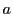 をとり,区間
をとり,区間![$I=[-a,\ a]$](images/img2551.gif) 上の連続関数空間を
上の連続関数空間を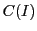 とする.
とする.
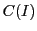 から
から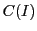 への写像
への写像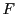 を
を
で定める.
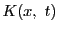 は連続であるから,
は連続であるから,
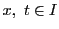 のとき
のとき
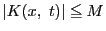 としてよい.
としてよい.
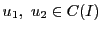 をとる.
をとる.
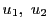 を
を
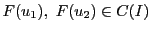 に変えてもよい.
に変えてもよい.
自然数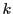 に対して
に対して
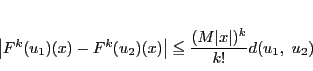 |
(10) |
と仮定すると,
より,数学的帰納法によって仮定10が一般に成り立つ.
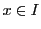 であるから
であるから
ところが
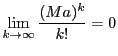 なので,
なので,
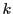 を大きくとることにより
を大きくとることにより
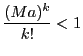 にとることができる.
にとることができる.
この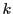 について
について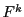 は
は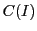 の縮小写像であり,
定理72によって
の縮小写像であり,
定理72によって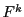 はただ一つの不動点
はただ一つの不動点
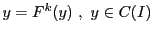 をもつ.
このとき
をもつ.
このとき
となり,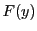 も
も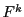 の不動点である.
の不動点である.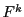 の不動点は一意であるから,
の不動点は一意であるから,
であり.つまり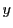 は
は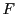 の不動点である.
の不動点である.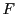 の不動点は
の不動点は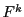 の不動点でもあるから,
一意である.よって
の不動点でもあるから,
一意である.よって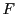 はただ一つの不動点
はただ一つの不動点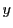 をもつことが示された.
をもつことが示された.
いいかえると任意の正数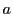 に対して,
積分方程式9の解
に対して,
積分方程式9の解
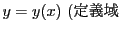 I=[-a, a]
I=[-a, a]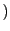 が一意に存在することが示された.
が一意に存在することが示された.
これは微分方程式8に対して,
![$I=[-a,\ a]$](images/img2551.gif) で定義され
で定義され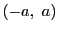 で微分可能な解が存在することを意味している.
□
で微分可能な解が存在することを意味している.
□
実数の完備性にはじまり微分方程式の解の存在に至る道を,
とにかく歩き通すことができた.
二階線形微分方程式の解の集合は空ではない.解の集合の構造を考えよう.
特に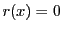 であるものを同次方程式という.
これに関して次の定理が成り立つ.
であるものを同次方程式という.
これに関して次の定理が成り立つ.
証明
(1)
より,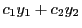 も解である.
も解である.
(2)
任意の解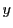 をとる.
行列
をとる.
行列
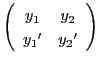 は,
は,
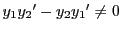 より逆行列をもつ.
そこで
より逆行列をもつ.
そこで
とおく.つまり
より
となる.第一式を微分して
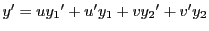 となる.
第二式と比較して
となる.
第二式と比較して
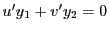 となる.
第二式を微分して
となる.
第二式を微分して
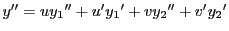 となる.
ここで
となる.
ここで
したがって
となる.つまり
である.
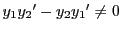 より
より
を得る.つまり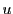 と
と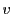 は定数である.よってこれを
は定数である.よってこれを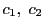 とおくと
とおくと
と表された.
□
実数で定義され二階微分可能な実数値関数の集合を とおく.
とおく.
 は実数上のベクトル空間である.
は実数上のベクトル空間である.
 から
から への写像
への写像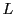 を
を
で定める.定理の証明と同様に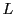 は
は の線型写像である.
定理86は
の線型写像である.
定理86は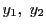 が
が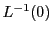 の基底となるための条件を示している.
の基底となるための条件を示している.
微分方程式
の解とは,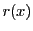 の原像
の原像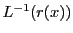 に他ならない.従って一つの解
に他ならない.従って一つの解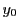 が求まれば,他の解はすべて
が求まれば,他の解はすべて
で得られる.
常微分方程式の実用的な解法については,多くの参考書がある.


 次: 惑星の運動
上: 微分方程式
前: 解の存在定理
次: 惑星の運動
上: 微分方程式
前: 解の存在定理
2014-05-23
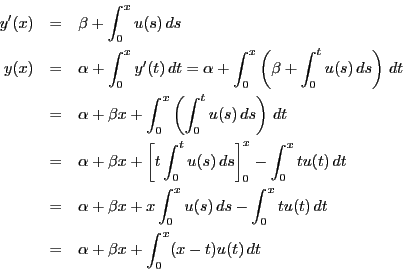
![]() が決定できればよい.
積分変数をそろえて微分方程式に代入する.
が決定できればよい.
積分変数をそろえて微分方程式に代入する.
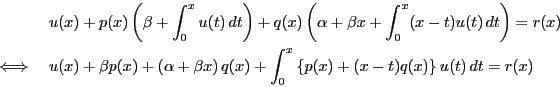
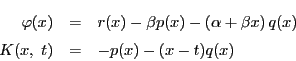
![]() をとり,区間
をとり,区間![]() 上の連続関数空間を
上の連続関数空間を![]() とする.
とする.
![]() から
から![]() への写像
への写像![]() を
を
![]() は連続であるから,
は連続であるから,
![]() のとき
のとき
![]() としてよい.
としてよい.
![]() をとる.
をとる.
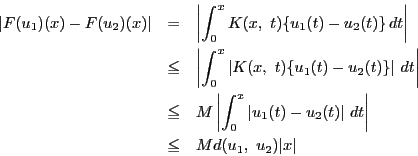
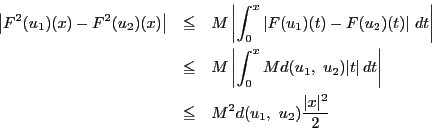
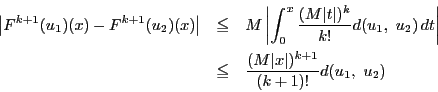
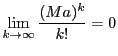 なので,
なので,
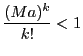 にとることができる.
にとることができる.
![]() について
について![]() は
は![]() の縮小写像であり,
定理72によって
の縮小写像であり,
定理72によって![]() はただ一つの不動点
はただ一つの不動点
![]() をもつ.
このとき
をもつ.
このとき
![]() に対して,
積分方程式9の解
に対して,
積分方程式9の解
![]() I=[-a, a]
I=[-a, a]![]() が一意に存在することが示された.
が一意に存在することが示された.
![]() で定義され
で定義され![]() で微分可能な解が存在することを意味している.
□
で微分可能な解が存在することを意味している.
□
![]() であるものを同次方程式という.
これに関して次の定理が成り立つ.
であるものを同次方程式という.
これに関して次の定理が成り立つ.
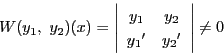
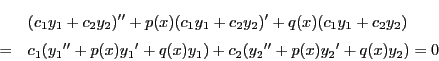
![]() をとる.
行列
をとる.
行列
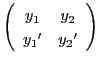 は,
は,
![]() より逆行列をもつ.
そこで
より逆行列をもつ.
そこで
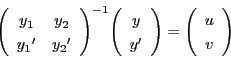
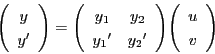
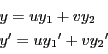
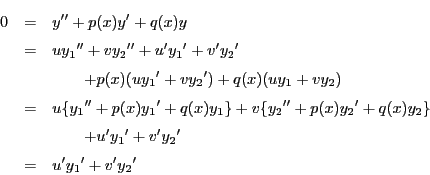
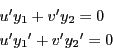
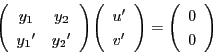
![]() とおく.
とおく.
![]() は実数上のベクトル空間である.
は実数上のベクトル空間である.
![]() から
から![]() への写像
への写像![]() を
を