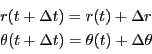次: 楕円軌道
上: 惑星の運動
前: 運動方程式
次: 楕円軌道
上: 惑星の運動
前: 運動方程式
これからは,太陽を原点とするある平面で考えればよいことになった.
ここでベクトル
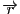 を
を
と極座標で表そう.ここで
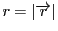 としている.
としている.
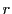 も角
も角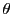 も時
も時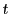 の関数であるとして,
速度ベクトルと加速度ベクトルを求めなければならない.
の関数であるとして,
速度ベクトルと加速度ベクトルを求めなければならない.
この結果は
と書ける.
ここで
である.だからまとめると,
ニュートンの法則は惑星運動では
となる.
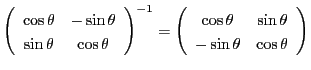 を左からかけると,
を左からかけると,
これから
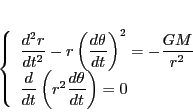 |
(13) |
を得る.
等式13から
が得られる.
極方程式で表された運動の,面積速度の式を求めよう.
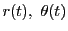 に対し時間の変化量を
に対し時間の変化量を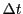 とし.
とし.
とおこう.また,動径の通過面積を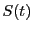 とする.
時間
とする.
時間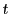 から
から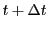 までの間の動径の最大値と最小値を
までの間の動径の最大値と最小値を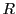 と
と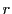 とすれば
とすれば
である. したがって
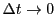 のとき
のとき
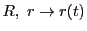 なので
なので
となる.
かくしてケプラーの第二法則:面積速度一定が示された.
2014-05-23
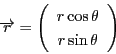
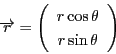
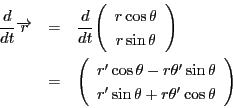
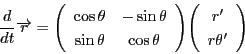
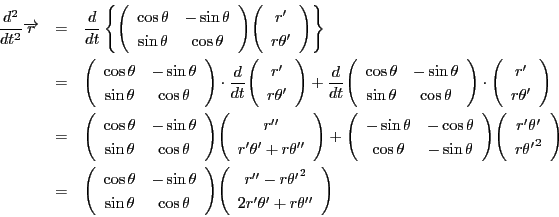
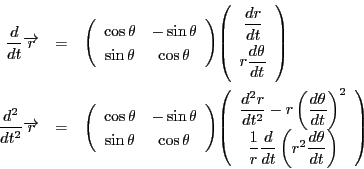
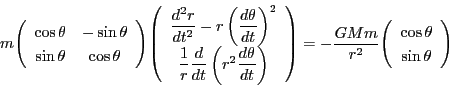
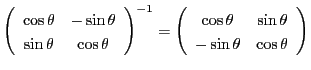 を左からかけると,
を左からかけると,
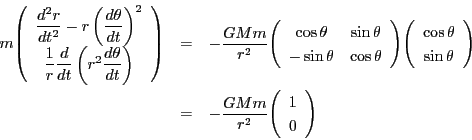
![]() に対し時間の変化量を
に対し時間の変化量を![]() とし.
とし.