九州大解答 問題に戻る 解説に進む 2000年入試に戻る
- 1.
z9=-1 である.また
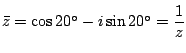 である.
である.
z9+1=(z3+1)(z6-z3+1) で
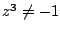 なので
なので
つまり 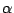 は
は
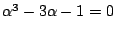 を満たすので
を満たすので
x3-3x -1=0
の解である.
- 2.
f(x)=x3-3x -1 とおく.
f'(x)=3x2-3 より f'(x)=0 の解は
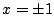
であるから, f(x)=0 は異なる3実数解を持つ.
有理数解
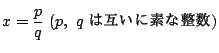 を持つとする.
を持つとする.
より
p3-3pq2-q3=0
これから
p,qは互いに素な整数なので p=q=1 .しかし x=1 は明らかに解でない.よって有理数の解はない.
- 3.
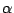 が2次方程式
が2次方程式
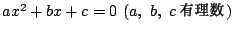 の解とする.
の解とする. 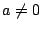 なので a で割ることにより
なので a で割ることにより
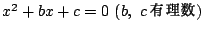 の解とできる.
の解とできる.
x3-3x-1=(x2+bx+c)(x-b)+(b2-c-3)x+bc-1
より
つまり
第1の場合 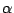 は有理数であり得ないことに反する.
は有理数であり得ないことに反する.
第2の場合
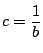 より
より
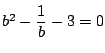 .つまり
.つまり
b3-3b-1=0
b が
x3-3x -1=0 の解である.ところが
x3-3x -1=0 は有理数の解を持ち得ないのであるから, b が有理数であることと矛盾した.
よって有理数を係数とする2次方程式で, 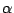 を解とするものは存在しないことが示された.
を解とするものは存在しないことが示された.
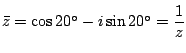 である.
である.
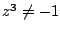 なので
なので
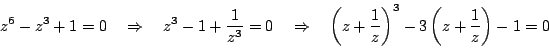
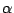 は
は
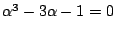 を満たすので
x3-3x -1=0
を満たすので
x3-3x -1=0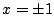
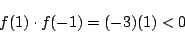
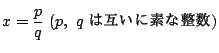 を持つとする.
を持つとする.
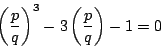
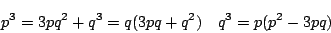
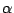 が2次方程式
が2次方程式
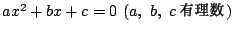 の解とする.
の解とする. 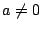 なので a で割ることにより
なので a で割ることにより
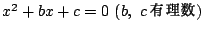 の解とできる.
の解とできる.
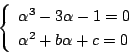 x3-3x-1=(x2+bx+c)(x-b)+(b2-c-3)x+bc-1
x3-3x-1=(x2+bx+c)(x-b)+(b2-c-3)x+bc-1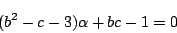
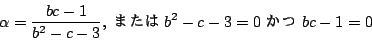
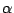 は有理数であり得ないことに反する.
は有理数であり得ないことに反する.
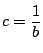 より
より
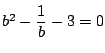 .つまり
b3-3b-1=0
.つまり
b3-3b-1=0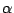 を解とするものは存在しないことが示された.
を解とするものは存在しないことが示された.