京大理系前期5 問題 解説 2001年入試に戻る
- (1)
条件(イ)より zk は1と異なる1の p 乗根である.
とおくと, 1と異なる1の p 乗根は
一意に表される.
このとき条件(ロ)は
となる.
an は の解
の解
の個数を表す.
であるから,
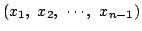 を
を
 が
pの倍数でないようにさえ選べば,一組の解が得られる.
が
pの倍数でないようにさえ選べば,一組の解が得られる.
ここで a2 を求める. a2 はx1+x2 がpの倍数となる
の p-1 個である.
a2=
p-1
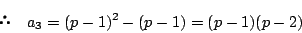
- (2)
(1)から
- (3)
を解く. 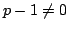 なので
なので
これから
[漸化式の別解]
の解を二つに分類する.
(i)
xn+1+xn+2 がpの倍数のとき.この
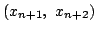 は a2=p-1
個ある.それぞれに対し
は a2=p-1
個ある.それぞれに対し
となる.x1+x2+…+xn の部分の決め方はan通りある.ゆえにこの場合の個数は
- (ii)
xn+1+xn+2 がpの倍数でないとき.
yn+1=xn+1+xn+2
とおくと
の解は an+1 個ある.
各 yn+1 に対して
yn+1=xn+1+xn+2+(pの倍数)
となる
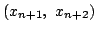 は p-1 組ある.
は p-1 組ある.
なぜなら xn+1 はyn+1
と同じにはとれない(同じにとるとxn+2がとれない)が,逆に異なれば
yn+1-xn+1と p で割ったの余りが等しいxn+2が一つ定まる.
ゆえにこの場合の個数は

それぞれは排反事象である.
 が
pの倍数でないようにさえ選べば,一組の解が得られる.
が
pの倍数でないようにさえ選べば,一組の解が得られる.
![]()
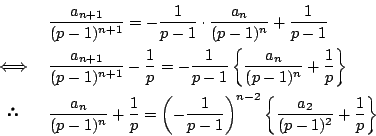
 が
pの倍数でないようにさえ選べば,一組の解が得られる.
が
pの倍数でないようにさえ選べば,一組の解が得られる.
![]()
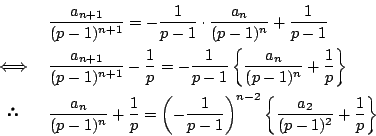
![]() は a2=p-1
個ある.それぞれに対し
は a2=p-1
個ある.それぞれに対し

![]()