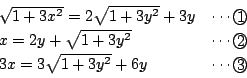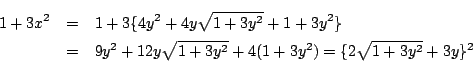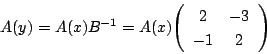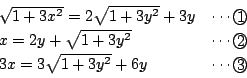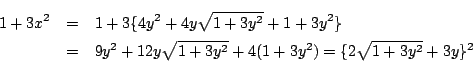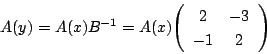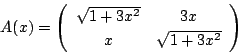次: 金沢後期理系 上: 解答 前: 慶応医

金沢前期理系

(1)

A(x)=A(y)B より各成分を比較して，

$$\begin{array}{ll} \sqrt{1+3x^2}=2\sqrt{1+3y^2}+3y&\cdots\mar... ...s\maru{2}\\ 3x=3\sqrt{1+3y^2}+6y&\cdots\maru{3} \end{array}$$

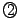$\maru{2}$ が成り立っているとき，

$$\begin{eqnarray*}1+3x^2&=&1+3\{4y^2+4y\sqrt{1+3y^2}+1+3y^2\}\\ &=&9y^2+12y\sqrt{1+3y^2}+4(1+3y^2)=\{2\sqrt{1+3y^2}+3y\}^2 \end{eqnarray*}$$

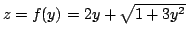よって， $\maru{2}$ を満たす正の x が存在すれば， それは $\maru{1},\ \maru{3}$ を満たす． $z=f(y)=2y+\sqrt{1+3y^2}$ とおく． f(y) は y に関する単調増加関数で f(0)=1 ．さらに f(y)>y である． したがって x>1 のとき，z=f(y)と z=x は yz 平面で y 座標が 0<y₀<x である点で交わる． つまり題意をみたす y がただ一つ存在する．

(2)

A(x)=A(y)B のとき，

$$A(y)=A(x)B^{-1}=A(x)\matrix{2}{-3}{-1}{2}$$

である． よってA(x) の各成分が自然数なら，0<y<x より行列 A(y) の各成分も自然数で ある． y>1 なら同じ操作をくり返す．今 A(y_k)=A(x)B^-k とおく． y_k>0 であるが さらにy_k>1 であるかぎり y_k>y_k+1 となる．

$$y_1>y_2>\cdots>0$$

が得られる．自然数の単調減少列なので 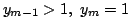$y_{m-1}>1,\ y_m=1$ となる k=m が存在する． つまり A(y_m)=A(x)B^-mで A(y_m)=A(1)=Bより A(x)=B^m+1． ゆえに n=m+1 とおくと確かに A(x)=Bⁿ となる自然数 n が存在した．

注

$$A(x)=\matrix{\sqrt{1+3x^2}}{3x}{x}{\sqrt{1+3x^2}}$$

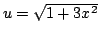で $u=\sqrt{1+3x^2}$ とおくと

u²-3x²=1

となる．つまり A(x) で x が自然数のとき，その1-1成分と1-2成分 は，ペル方程式

X²-3Y²=1

の自然数解になっている．

これは構造定理の別解になっている．